2019 VERSION: Volume III: Guidelines for Applying Traffic Microsimulation Modeling Software 2019 Update to the 2004 Version

2004 Version - 5.0 Calibration of Microsimulation Models

Upon completion of the error-checking task, the analyst has a working model. However, without calibration, the analyst has no assurance that the model will correctly predict traffic performance for the project.

Calibration is the adjustment of model parameters to improve the model's ability to reproduce local driver behavior and traffic performance characteristics. Calibration is performed on various components of the overall model.

The importance of calibration cannot be overemphasized. Recent tests of six different software programs found that calibration differences of 13 percent in the predicted freeway speeds for existing conditions increased to differences of 69 percent in the forecasted freeway speeds for future conditions.³⁴

5.1 Objectives of Calibration

Calibration is necessary because no single model can be expected to be equally accurate for all possible traffic conditions. Even the most detailed microsimulation model still contains only a portion of all of the variables that affect real-world traffic conditions. Since no single model can include the whole universe of variables, every model must be adapted to local conditions.

Every microsimulation software program comes with a set of user-adjustable parameters for the purpose of calibrating the model to local conditions. Therefore, the objective of calibration is to find the set of parameter values for the model that best reproduces local traffic conditions.

For the convenience of the analyst, the software developers provide suggested default values for the model parameters. However, only under very rare circumstances will the model be able to produce accurate results for a specific area using only the default parameter values. The analyst should always perform some calibration tests to ensure that the coded model accurately reproduces local traffic conditions and behavior.

The fundamental assumption of calibration is that the travel behavior models in the simulation model are essentially sound.³⁵  There is no need to verify that they produce the correct delay, travel time, and density when they are given the correct input parameters for a link. Therefore, the only remaining task for the analyst is to adjust the parameters so that the models correctly predict local traffic conditions.

5.2 Calibration Approach

Calibration involves the review and adjustment of potentially hundreds of model parameters, each of which impacts the simulation results in a manner that is often highly correlated with that of the others. The analyst can easily get trapped in a never-ending circular process, fixing one problem only to find that a new one occurs somewhere else. Therefore, it is essential to break the calibration process into a series of logical, sequential steps -- a strategy for calibration.

To make calibration practical, the parameters must be divided into categories and each category must be dealt with separately. The analyst should divide the available calibration parameters into the following two basic categories:

• Parameters that the analyst is certain about and does not wish to adjust.
• Parameters that the analyst is less certain about and willing to adjust.

The analyst should attempt to keep the set of adjustable parameters as small as possible to minimize the effort required to calibrate them. Whenever practical, the analyst should use observed field data to reflect local conditions. This observed data will serve as the nonadjustable values for certain calibration parameters, thus leaving the set of adjustable parameters to a minimum. However, the tradeoff is that more parameters allow the analyst more degrees of freedom to better fit the calibrated model to the specific location.

The set of adjustable parameters is then further subdivided into those that directly impact capacity (such as mean headway) and those that directly impact route choice. The capacity adjustment parameters are calibrated first, then the route choice adjustment parameters are calibrated.

Each set of adjustable parameters can be further subdivided into those that affect the simulation on a global basis and those that affect the simulation on a more localized basis. The global parameters are calibrated first. The local link-specific parameters are used after the global calibration to fine-tune the results.

The following three-step strategy is recommended for calibration:

1. Capacity Calibration: An initial calibration is performed to identify the values for the capacity adjustment parameters that cause the model to best reproduce observed traffic capacities in the field. A global calibration is performed first, followed by link-specific fine-tuning. The HCM can be used as an alternative source of capacity target values if field measurements are not feasible.
2. Route Choice Calibration: If the microsimulation model includes parallel streets, then route choice will be important. In this case, a second calibration process is performed, but this time with the route choice parameters. A global calibration is performed first, followed by link-specific fine-tuning.
3. System Performance Calibration: Finally, the overall model estimates of system performance (travel times and queues) are compared to the field measurements for travel times and queues. Fine-tuning adjustments are made to enable the model to better match the field measurements.

5.3 Step 1: Calibration for Capacity

The capacity calibration step adjusts the global and link-specific capacity-related parameters in the simulation model to best replicate local field measurements for capacity. This is an important step because capacity has a significant effect on predicted system performance (delay and queues).³⁶  The objective of this calibration step is to find a set of model parameters that causes the model to come as close as possible to matching the field measurements for traffic capacity.

The capacity calibration step consists of two phases: (1) a global calibration phase and (2) a fine-tuning phase. Global calibration is first performed to identify the appropriate network-wide value of the capacity parameter(s) that best reproduces conditions in the field. Link-specific capacity parameters are then adjusted to fine-tune the model so that it more precisely matches the field-measured capacities at each bottleneck.³⁷

The capacity calibration procedure is as follows:

1. Collect field measurements of capacity.
2. Obtain model estimates of capacity.
3. Select calibration parameters.
4. Set calibration objective function.
5. Perform search for optimal parameter value.
6. Fine-tune the calibration.

The following subsections explain this procedure in more detail.

5.3.1 Collect Field Measurements of Capacity

The identification of locations for field measurements of capacity will depend on the existing traffic conditions within the study area.

For nonsignalized facilities (freeways, rural highways, and rural roads), the analyst should identify locations where queues persist for at least 15 min and measure the flow rate at the point where the queue discharges. This observed flow rate is measured only while an upstream queue is present. It is totaled across all lanes and converted to an equivalent hourly flow rate. This is the field-measured capacity of the facility at this point.

For signalized intersections, the analyst should identify the approach legs that frequently have queues of at least 10 vehicles per lane and measure the saturation flow rate per hour per lane using the procedures outlined in Appendix H to the signalized intersection chapter of HCM. The capacity of the signalized intersection approach is then the saturation flow multiplied by the portion of green time in the signal cycle:

(Equation 2)

where:

c = capacity (vehicles per hour (veh/h))

s = saturation flow (veh/h per green phase)

g = effective green time

C = cycle length

Higher saturation flows and lower startup lost times result in higher capacities.

Several measurements of maximum flow rates should be made in the field and averaged. Procedures are provided in the appendix for estimating how many measurements are required to estimate capacity within a desired confidence interval (see Appendix B: Confidence Intervals). If capacity cannot be measured in the field, then the HCM methodology can be used to estimate capacity. The HCM methods should not be considered a default technique since the estimates are not as accurate as direct field measurements.

5.3.2 Obtain Model Estimates of Capacity

Microsimulation models do not output a number called "capacity." Instead, they output the number of vehicles that pass a given point. Thus, the analyst must manipulate the input demand as necessary to create a queue upstream of the target section to be calibrated so that the model will report the maximum possible flow rate through the bottleneck.

If the model does not initially show congestion at the same bottleneck locations as exist in the field, then the demands coded in the model are temporarily increased to force the creation of congestion at those bottlenecks. These temporary increases must be removed after the capacity calibration has been completed, but before the route choice calibration step.

If the model initially shows congested bottlenecks at locations that DO NOT exist in the field, it will be necessary to temporarily increase the capacity at those false bottlenecks (using temporary link-specific headway adjustments). These temporary adjustments are then removed during the fine-tuning phase.

For nonsignalized facilities (freeways, rural highways, and rural roads), the simulated queue should persist for at least 15 min of simulated time, across all lanes and links feeding the target section. The simulated capacity is then the mean flow rate at the target section (measured at a detector placed in the target section and summed across all lanes) averaged over the 15-min or longer period that the queue is present. The result is then divided by the number of lanes and is converted to an hourly flow rate.

For signalized intersections, the coded demand should be increased, as necessary, to ensure the necessary queues of at least 10 vehicles at the start of the green phase. A detector is placed in the model at the stop line to measure the discharge headways (on a per lane basis) of the first 10 vehicles crossing the detector in each lane.³⁸  The per lane headways are averaged for each lane and then averaged across lanes. The result is then converted to an hourly flow rate per lane.

Just as the field measurements of capacity were repeated several times and the results were averaged, the model runs should be repeated several times and the maximum flow rate at each location should be averaged across the runs. The minimum required number of runs to obtain a value of capacity within a desired confidence interval can be calculated using the procedures provided in Appendix B (Confidence Intervals).

5.3.3 Select Calibration Parameter(s)

Only the model parameters that directly affect capacity are calibrated at this time. Each microsimulation software program has its own set of parameters that affect capacity, depending on the specific car-following and lane-changing logic implemented in the software. The analyst must review the software documentation and select one or two of these parameters for calibration.

This chapter does not intend to describe all of the parameters for all of the simulation models that are available. An illustrative list of capacity-related parameters for freeways and signalized arterials is given below:

Freeway Facilities:

• Mean following headway.
• Driver reaction time.
• Critical gap for lane changing.
• Minimum separation under stop-and-go conditions.

Signalized Intersections:

• Startup lost time.
• Queue discharge headway.
• Gap acceptance for unprotected left turns.

For example, in CORSIM, the two parameters that most globally affect capacity are "headway factor by vehicle type" (record type 58) and "car following sensitivity factor" (record type 68). There are numerous other parameters in CORSIM that affect capacity; however, they mostly apply only to specific conditions (e.g., "acceptable gap in near-side cross traffic for vehicles at a stop sign" (record type 142)).

For the fine-tuning phase in CORSIM, the link-specific capacity calibration parameter is "mean queue discharge headway," which can be found in record type 11 for city streets, and in record type 20 for freeways ("link-specific car-following sensitivity multiplier").

5.3.4 Set Calibration Objective Function

It is recommended that the analyst seek to minimize the mean square error (MSE) between the model estimates of maximum achievable flow rates and the field measurements of capacity. The MSE is the sum of the squared errors averaged over several model run repetitions. Each set of repetitions has a single set of model parameter values p with different random number seeds³⁹ for each repetition within the set.⁴⁰

Select a set of model parameters p to minimize:

(Equation 3)

Subject to:

for all user-adjustable model parameters pm

where:

MSE = mean square error

M_ltpr = model estimate of queue discharge flow rate (capacity) at location l and time t, using parameter set p for repetition r

F_l = field measurement of queue discharge flow rate (capacity) at location l

R = number of repetitive model runs with fixed parameter values pm and different random number seeds⁴¹

p_m = value of model parameter number m

p_m^min, p_m^max = user-specified limits to the allowable range of parameter values pm (limits are necessary to avoid solutions that violate the laws of physics, vehicle performance limits, and driver behavior extremes)

5.3.5 Perform Search for Optimal Parameter Value

The analyst must now find the capacity adjustment factor(s) p that minimizes the MSE between the model and the field measurements of capacity. The calibration problem is a nonlinear least-squares optimization problem.

Since simulation models are complex, it is not usually possible to formulate the models as a closed-form equation for which traditional calculus techniques can be applied to find a minimum value solution. It is necessary to use some sort of search algorithm that relies on multiple operations of the simulation model, plotting of the output results as points, and searching between these points for the optimal solution. Search algorithms are required to find the optimal solution to the calibration problem.

There are many software programs available for identifying the optimal combination of calibration parameters for minimizing the squared error between the field observations and the simulation model. The Optimization Technology Center Web site of the Argonne National Laboratory and Northwestern University lists several software programs for nonlinear least-squares parameter estimation.

Appendix D describes a few simple search algorithms that can be applied manually or with the aid of spreadsheets. Figure 7 illustrates how a single parameter search (m = 1) might look using one of these simple search algorithms for the number of model runs (R) set to 4.

Figure 7. Minimization of MSE.

5.3.6 Fine-Tune the Calibration

Once the optimal global capacity calibration parameter values have been identified, there will still be some locations where model performance deviates a great deal from the field conditions. Therefore, the next phase is to fine-tune the predicted capacity to match the location-specific measurements of capacity as closely as possible.

Link-specific capacity adjustments account for roadside factors that affect capacity, but are not typically coded in the microsimulation network input data set (such as presence of onstreet parking, numerous driveways, or narrow shoulders). Most simulation software programs have link-specific capacity (or headway) adjustment factors that apply only to the subject link. These capacity adjustment factors are used to fine-tune the model calibration. Link-specific adjustment factors should be used sparingly since they are not behavior-based. They are fixed adjustments that will be carried through all future runs of the simulation model.

5.4 Step 2: Route Choice Calibration

Once the analyst is satisfied that the model reproduces as closely as possible the field-measured capacities, the next step is to then calibrate the route choice parameters in the model to better match the observed flows. The temporary demand adjustments used in the previous capacity calibration step are reversed. The model-predicted volumes are then compared to the field counts and the analyst adjusts the route choice algorithm parameters until the best volume fit is achieved.⁴²

If the model network consists of only a single facility, then no route choice calibration is possible or needed. This step is skipped.⁴³  This step is also skipped for microsimulation software that does not have route choice capabilities.

Route choice calibration proceeds in two phases: (1) global calibration and (2) link-specific fine-tuning.

5.4.1 Global Calibration

Global calibration of route choice consists of the application of a route choice algorithm and associated parameters.⁴⁴  The specific parameters vary by algorithm and software program, but usually involve weightings placed on the actual cost and travel time for each route. Additional parameters may be related to the familiarity of the driver with each route and the amount of error in the driver's perception of the cost and time for each route. The analyst must review the software documentation and select one or two of these parameters for calibration. Global calibration then proceeds through the same process as was used to calibrate capacity. The MSE between the field counts and the model volume estimates is minimized using one of the available nonlinear optimization techniques.

5.4.2 Fine-Tuning

Once the global calibration has been completed, link-specific adjustments to cost or speed are made during the fine-tuning phase. The fine-tuning has been completed when the calibration targets for volumes have been met (see section 5.6 on calibration targets).

5.5 Step 3: System Performance Calibration

In this last step of the calibration, the overall traffic performance predicted by the fully functioning model is compared to the field measurements of travel time, queue lengths, and the duration of queuing. The analyst refines link free-flow speeds and link capacities to better match the field conditions. Since changes made at this step may compromise the prior two steps of calibration, these changes should be made sparingly. The next section suggests calibration targets for this last step of the review.

5.6 Calibration Targets

The objective of model calibration is to obtain the best match possible between model performance estimates and the field measurements of performance. However, there is a limit to the amount of time and effort anyone can put into eliminating error in the model. There comes a point of diminishing returns where large investments in effort yield small improvements in accuracy. The analyst needs to know when to stop. This is the purpose of adopting calibration targets for the model.

Calibration targets are developed based on the minimum performance requirements for the microsimulation model, taking into consideration the available resources. The targets will vary according to the purpose for which the microsimulation model is being developed and the resources available to the analyst.

Table 4 provides an example of calibration targets that were developed by Wisconsin DOT for their Milwaukee freeway system simulation model. They are based on guidelines developed in the United Kingdom.⁴⁵

Another example of suggested calibration targets is "Theil's Inequality Coefficient," which is broken down into three parts, each of which provides information on the differences between the model measures and the target measures.⁴⁶

Table 4. Wisconsin DOT freeway model calibration criteria.

Source: "Freeway System Operational Assessment," Paramics Calibration and Validation Guidelines (Draft), Technical Report I-33, Wisconsin DOT, District 2, June 2002.

Note: The GEH statistic is computed as follows:

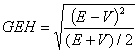(Equation 4)

where:

E = model estimated volume

V = field count

5.7 Example Problem: Model Calibration

The same example problem from the previous chapters is continued. The task is now to calibrate the model.

A review of the results produced by the working model at the end of the model development task indicates that there are discrepancies between the observed and simulated traffic performance. The purpose of the calibration process is to adjust the model parameters to better match field conditions.

Calibration for Capacity -- Step 1: Global Calibration

Field Data on Capacity: The network under study is not congested. Therefore, field measurements of the capacity values on the freeway links and saturation flows at the traffic signals on the arterials cannot be obtained.

Two potential future bottleneck locations were selected on the study area network. The capacities for these potential bottleneck locations were estimated using the HCM 2000 procedures. The estimated value for the saturation flow for protected movements at signalized intersections was 1800 vehicles per hour of green per lane (vphgpl) and the capacity of the freeway links was 2100 vphgpl.

Model Estimates of Capacity: The model estimates of capacity can be obtained from detector measurements or from the throughput values reported at the end of the simulation run. However, it is necessary to have upstream queues for the throughput values to represent capacity.

Because of the lack of congestion, the existing volumes on the network links had to be artificially increased to trigger congestion upstream of the bottleneck locations (the model throughput volumes at these bottleneck locations would then be the model-estimated capacities).

Select Calibration Parameters: The global parameter calibration was performed using the following parameters:

• Mean queue discharge headway at traffic signals: The default value for this parameter in the model is 1.8 s/veh (which is equivalent to a saturation flow of 2000 vphgpl under ideal conditions). The queue discharge headway per vehicle type is randomly assigned by the model, depending on the driver's aggressiveness factor.
• Mean headway (or car-following sensitivity factor) for the freeway links: This represents the minimum distance that a driver is willing to follow vehicles. The values of the headway (or sensitivity factors) depend again on driver aggressiveness. Lower values would cause higher throughput.

Set Calibration Objective Function: The criterion chosen to determine the optimal parameter value was the minimization of the MSE between the model estimates of saturation flow/capacity and the field estimates.

Table 5 shows the values of the mean queue discharge headway tested and the resulting simulated saturation flows. Ten replications for each assumed value of the parameter were performed to estimate the model-generated saturation flow within 5 percent of its true value. The mean values of the saturation flows were used in the calculation of MSE. Figure 8 shows the values of MSE for each parameter value. The results indicate that a value of 1.9 s produces the minimum MSE for this data set.

Table 5. Impact of queue discharge headway on predicted saturation flow.

Note: Each column labeled 1 through 10 represents a model run repetition using a different random number seed.

Figure 8. Impact of mean queue discharge headway on MSE of modeled saturation flow.

A similar procedure was followed for the calibration of the mean headway values for freeway links. Model runs were performed assuming higher through volumes on the network links.

The results indicated that the default minimum headway (car-following sensitivity factor in CORSIM) must be reduced by 5 percent (i.e., 95 percent of its default value for the model throughput to match the observed value of 2100 vphgpl). This value minimizes the MSE.

Figures 9 and 10 illustrate the effect of this parameter on freeway performance. Before calibration (Figure 9), the average speed on a series of freeway links is much lower than the speeds after calibration of the headways in the HCM 2000 (Figure 10).

Figure 9. Average speed by minute of simulation (three links): Before calibration.

Figure 10. Average speed by minute (three links): After calibration.

Calibration for Capacity -- Step 2: Fine-Tuning

For this example, field capacity measurements were only available for two links on the network -- one for the freeway and one for the surface street. These measures were used in the previous step to perform the global calibration. Given that no other field capacity data were available, no further fine-tuning (or link-level calibration) is needed.

Calibration for Route Choice

The prior calibration step has ensured that the model is predicting the correct capacities. With the correct capacities, the model should no longer have bottlenecks at the incorrect locations with too low or too high discharge rates. The upstream and downstream traffic volumes on each of the links should now better match the observed counts. Any remaining differences (assuming that error checking caught errors in the source node volumes) should be the result of route choice errors in the model. Therefore, the purpose of route choice calibration is to better match the counts at the non-bottleneck locations on the network.

The particular software selected for this example problem does not predict changes in route choice (no O-D table was provided for the model). Therefore, there is no route choice to be calibrated.⁴⁷  Assuming that the analyst is confident in the quality of the turn counts entered into the model (and converted inside the model into equivalent turn probabilities for routing traffic), any remaining errors in the link volumes can be corrected by manual adjustments to midblock source and sink node volumes.

In this example problem, the freeway, ramp, and intersection counts were all adjusted at the data preparation stage to produce an internally consistent set of volumes for every link and node. There are no unaccounted for increases or decreases in volumes between nodes. Thus, no midblock source/sink nodes were required. The model-predicted link volumes based on the source node volumes and the intersection turn percentages are consistent with the link counts (within the range of variation expected because of the random components of the simulation model).

System Performance Calibration

Once calibration has been completed to the analyst's satisfaction, the next step is to calibrate the overall performance of the model.

The model predictions were compared with the field data on speed, travel time, and delay on the freeways and arterials.

Based on this comparison, the free-flow speed distribution for the freeway was adjusted so that the model-generated free-flow speeds were within a more narrow range than the default distribution. This reflects commuter traffic behavior.

No other adjustments were made to the model parameters.

Ten repetitions of the calibrated data set were performed and the link output was processed to produce performance measures to be compared with the field data.

The comparison is shown in Table 6. The simulated values represent the mean value of the MOEs based on the 10 model runs for the third time slice of the simulated peak hour.

Comparisons with field measurement of delay are not shown here because it was unclear how the field data on delay were collected. In general, users must be cautious when they compare field versus simulated delays because the delay is typically defined differently in most software programs than in the approaches commonly used for field measurements.

The results indicate that the model satisfies the criteria for calibration (shown in Table 4).

Table 6. System performance results for example problem (freeway segment).

Table 6. System performance results for example problem (arterial segment).