SIGNAL TIMING UNDER SATURATED CONDITIONS

1. Literature Review

Overview

Considering the impact of oversaturated signals on motorist delay and network performance, surprisingly little research has been conducted that leads to specific and implementable methods to recommend to practitioners. Much of the literature that does exist is devoted to quantifying the queue that results when the green time is insufficient to serve the arrival demand. Most of this research has not been cited in this section. Work cited here provides some attempt at responding to the saturation problem rather than merely quantifying traffic flow in a signal-imposed queue.

In the early 1960's, Gazis studied oversaturated conditions and wrote the earliest papers found in the literature. He assumed that the time duration of the oversaturated period, the demand curve, and the service curve were empirically known and objective was to minimize the area between these two curves, which is a measure of the total delay. When the arrival demand cannot be served by the service curve, the two curves diverge and the amount of unserved queue grows. Many attempts have been made to characterize delay while considering the unserved queue. For example, a deterministic departure process leads to the following equation, as reported by Rouphail (1995):

The problem with this and other delay models is that they require knowledge of the residual queue size, Q_o. With a variable residual queue in the right-hand side of the equation, and delay on the left, delay cannot be calculated as a steady-state measure, and the equation has no closed-form solution without an assumption of the time period, and without disregarding the delay of the vehicles that remain in the residual queue at the end of that time period.

After Gazis's publication, a substantial effort to identify a closed-form analytical estimate of the residual queue ensued. These efforts failed in the general case, leading to the approach of developing computationally convenient delay models that could be evaluated at demand levels exceeding estimates of capacity. Modeling predictable values of delay when demand exceeds capacity was a compromise with reality, and the commitment to using delay as an optimization objective override the inability calculate delay in those conditions.

In Gazis's work, the resulting optimal control policy was constructed by dividing the oversaturated period into two stages, in the first stage, the maximum green is allocated to the phase with highest flow rate and the minimum green time is allocated to the other phase. In the second stage the maximum and minimum green times are switched, to oscillate between residual queues on the two approaches with the objective of balancing them. Thus, the objective of the approach was to balance queue formation. The optimal cycle length and switching point from stage to stage were calculated based on the traffic volumes and duration.

This basic approach was modified to include queue capacity constraints by Michalopoulos, Stephanopolos, and May (1978). More recently Chang and Lin (2000) developed a discrete state space version of Gazis's model. The advantage of the discrete model is that the switch point is always at the end of a cycle.

Daganzo (1995) introduced a Cell Transmission Model (CTM) to capture the dynamics of traffic flow. In the CTM the entire traffic network is divided into small cells with each cell length defined as the distance a vehicle can travel at free flow in one time step. Lo and others (2004) applied the CTM to oversaturated traffic networks with the objective to minimize the total delay of the whole network. Using the CTM approach, the delay for each time step is calculated as the number of vehicles occupying each cell minus the number of vehicles that exit the cell. It is assumed that the traffic volume is fully known in each cell. A genetic algorithm was used to solve the network model on a simple single-direction network.

Li and Prevedouros (2004) used a hybrid optimization and rule-based strategy to control an isolated oversaturated intersection. The queue length of each lane from each approach must be measured or known. Their objective was to maximize the throughput and control the queue length. The calculation was conducted and the signal updated at the end of the active phase. Each phase green time is allocated as the time needed to disperse the maximum lane queue length subject to the maximum phase length; also the total number of vehicles served was calculated for each phase and then divided by the phase green time to get the throughput. MOVA (1986) used a similar detection method for isolated intersection signal control.

Park, et al. (1999) formulated the traffic network as an optimization problem. The cycle length, offset, green split and phase sequence were the decision variables, and the objective was throughput maximization, average delay minimization and modified average delay minimization with a penalty function. They developed a genetic algorithm to solve the network optimization problem numerically, in the absence of a closed-form solution for delay.

Researchers have tried to improve the utilization of the capacity of an intersection to relieve the congestion problem. But in oversaturated conditions, even with efficient use of the intersection capacity, vehicles still accumulate in every subsequent cycle and the residual queue on these approaches will finally reach the upstream intersection.

There has been some research directed towards the minimization of the spreading of network congestion from an oversaturated intersection. This research has sought to identify and evaluate corrective methods for preventing upstream queue effects, and also to manage the effect of the departure flow on downstream signals. The concept of network queue management was formalized in the work by Lieberman et al. (1992, 2000) where the researchers first identified internal traffic metering to maintain stable queues in the congested network, and then developed a mixed-integer linear program to optimize the offsets. A nonlinear quadratic model was used to find the optimal phase durations. Arterial simulation was conducted with the WATSim micro simulation model to demonstrate the effectiveness of this approach compared to traditional signal timing models such as SYNCHRO, PASSER and TRANSYT that do not directly consider oversaturated movements and network congestion.

More recently, manufacturers have responded to suggestions from practitioners to provide features to address congested conditions, where traditional actuated fails. These methods are described in Chapter II, but one feature has been evaluated in recent research and should be mentioned here. Yun, et al. (2007) evaluated the dynamic maximum green in actuated controllers using hardware-in-the-loop simulation, finding that it outperforms commonly implemented alternatives. Essentially, this approach allows the maximum green time(s) of phases that serve oversaturated approaches to increase by some step size each cycle, up to some maximum total increase.

Among all these approaches, none except MOVA and the dynamic maximums are implemented outside the research context and few of those have moved beyond laboratory experimentation. None except the research into adaptive maximum green were developed in the context of current traffic control hardware, and most would require implementation at the system rather than intersection level. Many require detection capabilities that do not exist in practice, such as the ability to measure queue length.

Below is an annotated bibliography of papers referred to above that have addressed the issues of oversaturated intersections or congested networks, followed by a general list of references relevant to control methods at saturated intersections. The final section of this chapter includes a special discussion of NCHRP 3-66, which has reconsidered intersection control from the perspective of the latest detection capabilities.

Annotated Bibliography

Foundational Research

Gazis, D. C. and R.B. Potts, "The Oversaturated Intersection", Proceedings of the Second International Symposium on the Theory of Traffic Flow, London, England, 1963

Gazis, D. C., "Optimal Control of a System of Oversaturated Intersections", Operations Research Vol. 12, pp. 815-491, 1964.

The oversaturated isolated intersection control was first studied in this paper. The intersection under study consists of two phases with no turns, and assumed that the demand rate Q(t) is known and it follows a linear function. The method tries to minimize the total delay over the oversaturated period T. The resulting solution divided control into two stages over the time T, an optimal switchover time from stage one to stage two is found. In the first stage phase 1 is assigned maximum green time phase 2 is assigned minimum green time, while in the second stage the phase 1 is assigned minimum green time and phase 2 is assigned maximum green time. In Gazis (1964), this approach is extended to a system of oversaturated intersections. No simulation was conducted to study the performance of such control strategies.

Chang, Tang-Hsien and Jen-Ting Lin, "Optimal Signal Timing for an Oversaturated Intersection", Transportation Research Part B, Vol. 34, pp.471-491, 2000.

This paper reformulated the problem in Gazis (1963) using a discrete state space method and developed an algorithm to solve the model. In the discrete model the switchover time occurred exactly at the end of a cycle.

Optimization Model Research

Lo, Hong K., M.ASCE, and Andy H.F. Chow, "Control Strategies for Oversaturated Traffic", Journal of Transportation Engineering. August 2004.

This paper applied the Cell Transmission Model (CTM) to the control of oversaturated traffic network. The link between intersections is divided into cells with length of the travel distance at free flow speed, the number of vehicles in cell in each time step is monitored. Given this information the model optimize the signal of whole network. The genetic algorithm is used to find a near optimal solution; it is capable of generating variable green splits with no cycle plans. Simulation is conducted using a real traffic network consisting three intersections in Hong Kong and the result is compared with existing timing plan.

Hong Li and Panos D. Prevedouros. "Traffic Adaptive Control for Oversaturated Isolated Intersections: Model Development and Simulation Testing", .Journal of Transportation Engineering. Sep 2004

Traffic adaptive control for oversaturated intersections called TACOS is described and simulated. In this approach, there is no fixed cycle length, and phase sequence is dynamically assigned. The queue length on each lane must be estimated, and the phase green duration is calculated as the time needed to discharge the longest queue associated with that phase plus the time needed to service vehicles that joining the queue during the queue dissipation. The phase duration is also subject to min and max constraints. The method estimates the total number of vehicles to be serviced for each candidate phase, given phase green duration and total number of vehicles that need to be serviced for a phase. The algorithm calculates the throughput near the end of each phase, and chooses the next phase that provides the maximum throughput.

The algorithm is simulated in an environment called ICS which emulates NETSIM and INTEGRATION and was designed to be able to simulate the intersection operation under pretimed, actuated and TACOS control. The simulation compared the result of these three control strategies, claimed that the TACOS improve the performance significantly.

It is not known yet how TACOS performance compared to the other adaptive control strategies. But compared to some other adaptive control strategies, TACOS does not require the prediction algorithms which may introduce extra errors, even though prediction allows the controller to respond to the traffic proactively and therefore minimize the number of stops and delay.

TACOS did not address the solution for coordination if there is a need to be extended to arterial or network environment. The algorithm was designed only for congested conditions, and was not evaluated for sub-capacity conditions.

Yun, Ilsoo Matthew Best, and Byungkyu "Brian" Park. "Evaluation of the Adaptive Maximum Feature in the EPAC300 Actuated Traffic Controller Using hardware-in-the-Loop Simulation", TRB poster session, 2007

When operating under heavy traffic volume from all approaches, an actuated controller tends to function as a fixed time controller with maximum green time on saturated approaches. With adaptive max, the max green is incrementally changed according to the gap out information. Contiguous maxing out results in increasing max times, and contiguous gapping out results in decreasing max times. By using this method, more green time could be allocated to the saturated approaches, thus reducing the congestion. This paper evaluated adaptive max scenarios and identified research problems for dynamic max, such as the appropriate step size and upper and lower bounds of the resulting maximum green value. Simulation was conducted using hardware in the loop with VISSIM. The adaptive maximum was compared to two other alternatives: an arbitrarily large maximum green and the maximum green suggested by SYNCHRO. The result showed the adaptive maximum resulted in improved performance.

Network Metering

Edward B. Lieberman and Carroll J. Messer. NCHRP 3-38(4) Final Report: Internal Metering Policy for Oversaturated Networks. TRB, National Research Council, Washington DC, 1992

Edward B. Lieberman, Jinil Chang, and Elena Shenk Prassas. "Formulation of Real-Time Control Policy for Oversaturated Arterials", Transportation Research Record 1727, TRB, National Research council, Washington,D.C., 2000 pp.77-88

In this work, researchers formulated a control policy they called IMPOST, which implements an approach for metering traffic into congested intersections. The objectives are maximization of system throughput, full use of storage capacity to control the queue growth, and equitable service to cross street traffic and left turn traffic. A mixed-integer linear program (MILP) is used to find optimal signal offsets and queue length for each approach. A separate quadratic programming model is used to adjust the arterial green phase durations of each signal cycle so that the actual arterial queue lengths on each saturated approach will continually and closely approximate the optimal queue length computed by the MILP formulation. The simulation compared four different signal timing tools, including IMPOST, PASSER, TRANSYT, and SYNCHRO. The result showed that the IMPOST policy yielded improved network travel speed and delay under congested conditions.

Genetic Algorithms

Byungkyu "Brian" Park, Carroll J. Messer, and Thomas Urbanik. "Traffic Signal Optimization Program for Oversaturated Conditions - Genetic Algorithm Approach", Transportation Research Record 1683, TRB, National Research council, Washington, D.C., 1999 pp. 133-141

Byungkyu "Brian" Park, Carroll J. Messer, and Thomas Urbanik "Enhanced Genetic Algorithm for Signal Timing Optimization of Oversaturated Intersections", Transportation Research Record 1727, TRB, National Research council, Washington,D.C., 2000 pp. 32-41

The program tries to optimize the cycle length, phase split, phase sequence, and offset simultaneously by using a genetic algorithm. The objective function value is evaluated using a mesoscopic simulator instead of an explicit deterministic objective function. The program considers the optimization of the four parameters of each intersection in a network. The paper compared the genetic algorithm approach with TRANSYT-7F optimization evaluated using CORSIM. The research showed that for low, medium and high flow conditions, the genetic algorithm performed best in low and high conditions, and performed as well as TRANSYT-7F in medium flow conditions.

In the second paper, the objective function is modified to prevent the low demand movements from being unrealistically delayed.

MCH1542 B Installation Guide for MOVA

MOVA was developed by the Transport Research Laboratory (now the Transport and Road Research Laboratory) to specifically address isolated intersection control. The MOVA controller, though not compatible with U.S.-style signal controllers, has been deployed in the field in England and other countries throughout the world.

The controller uses different strategies for undersaturated and oversaturated conditions. In the undersaturated condition the goal is minimization of vehicle delay and vehicle stops for the whole intersection. In the oversaturated condition the objective is to maximize the capacity on the congested approaches.

The controller uses lane-based detection. Two detectors are needed for each lane within a specified travel time from the detectors to the stop line at cruise speed. The first one is 8 seconds and second one is 3.5 seconds. The controller primary has a preset sequence of stages, depending on demand the stage maybe skipped.

MOVA's logic checks if any approaches are saturated, and if so maximum green time will be allocated to that approach. MOVA includes logic to determine the green duration of other non-saturated approaches in such a way that the green time is efficiently used.

Red Clearances

Two studies have been conducted that suggest that there is no longer term net benefit to increasing red clearances beyond the normal practice of providing clearance time across the intersection. Increases in red clearances were noted later in this project to have a disproportionate effect on congested movements, as explained in Chapter II. These studies include:

Roper, Brian A., Jon D. Fricker, C. Sinha Kumares, Robert E. Montogomery. The effects of the All-Red Clearance Interval on Intersection Accident Rates in Indiana. Report No. FHWA/IN/JHRP-90/7, Indiana Department of Transportation. http://ntlsearch.bts.gov/tris/record/tris/00623613.html

Reginald R. Souleyrette, et. al, Effectiveness of All-Red Clearance Interval on Intersection Crashes, Report No. MN/RC-2004-26, Minnesota Department of Transportation, May 2004. www.lrrb.org/PDF/200426.pdf

References

Abu-Lebdeh, Ghassan and Rahim F. Benekohal. "Genetic Algorithm for Traffic Signal Control and Queue Management of Oversaturated Two-Way Arterials" In Transportation Research Record: Journal of the Transportation Research Board No.1727, TRB, National Research Council, Washington, DC, 2000, pp.61-67

Abu-Lebdeh, Ghassan and Rahim F. Benekohal. "Signal Coordination and Arterial Capacity in Oversaturated Conditions" In Transportation Research Record: Journal of the Transportation Research Board No.1727, TRB, National Research Council, Washington, DC, 2000, pp.68-76

Abu-Lebdeh, Ghassan and Rahim F. Benekohal. "Design and evaluation of dynamic traffic management strategies for congested conditions" Transportation Research Part A 37 2003, pp.109-127

Chang, Tang-Hsien and Jen-Ting Lin. "Optimal signal timing for an oversaturated intersection" Transportation Research Part B 34, 2000, pp. 471-491 

Choi, B.K. Adaptive Signal Control for Oversaturated Arterials, Ph.D. Dissertation. Polytechnic University, Brooklyn, NY, 1997

Daganzo, C.F. "The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory." Transportation research part B 28B(4), 1995, pp. 269-287

Gazis, D. C. and R.B. Potts. "The Oversaturated Intersection" Proceedings from the Second International Symposium on the Theory of Traffic Flow, London, England, 1963, pp. 222-237.

Gazis, D. C. "Optimal Control of a System of Oversaturated Intersections" Operations Research 12, 1964, pp. 815-491.

Li, Hong and Panos D. Prevedouros. "Traffic Adaptive Control for Oversaturated Isolated Intersections: Model Development and Simulation Testing" Journal of Transportation Engineering. September 2004, pp. 594-601

Lieberman, Edward B., A.K. Rathi, G.F. King, and S.I. Schwartz. "Congestion-Based Control Scheme for Closedly Spaced, High Traffic Density Networks" In Transportation Research Record: Journal of the Transportation Research Board No.1057, TRB, National Research Council, Washington, DC, 1986, pp.49-57

Lieberman, Edward B. and Carroll Messer. Internal Metering Policy for Oversaturated Networks—Final Report. Project 3-39(4), National Cooperative Highway Research Program, TRB, National Research Council, Washington, DC, 1992

Lieberman, Edward B., Jinil Chang, and Elena Shenk Prassas, "Formulation of Real-Time Control Policy for Oversaturated Arterials". In Transportation Research Record: Journal of the Transportation Research Board No. 1727, TRB, National Research Council, Washington, D.C., 2000, pp.77-88

Lo, Hong K. and Andy H. F. Chow. "Control Strategies for Oversaturated Traffic", Journal of Transportation Engineering. American Society of Civil Engineers, August 2004, pp. 466-478.

Michalopoulos, P.G., Stephanopolos, G., "Optimal control of oversaturated intersections theoretical and practical considerations," Traffic Engineering & Control. May 1978, pp. 216-221

MCH1542 B Installation and Application Guide for MOVA

Park, Byungkyu, Carroll J. Messer, and Thomas Urbanik. "Enhanced Genetic Algorithm for Signal Timing Optimization of Oversaturated Intersections." Transportation Research Record No. 1727, TRB, National Research Council, Washington, DC,2000, pp.32-41

Rouphail, Nagui, Andrzej Tarko and Jing Li, "Traffic Flow at Signalized Intersections" Traffic Flow Theory Monograph, ed. Nathan Gartner and Carroll Messer. First draft, printed for Federal Highway Administration by Oak Ridge National Laboratory, 1995.

Yun, Ilsoo, Matthew Best, and Byungkyu Park. "Evaluation of the Adaptive Maximum Feature in the EPAC300 Actuated Traffic Controller Using hardware-in-the-Loop Simulation", TRB poster session 2007

Overview of NCHRP 3-66

The NCHRP 3-66 project entitled Traffic Signal State Transition Logic Using Enhanced Sensor Information focused on three related issues in traffic signal control. First, an architecture for traffic signal control logic was developed to support the discussion and development of logic. Next, a model of the core traffic signal controller logic was developed and used to show how single and multiple priority requests can be served and how the different phase intervals, minimum, pedestrian, etc. relate to the signal timing logic. The role and use of traffic signal detectors was investigated and improved detection information was defined and linked to the controller core logic. Finally, the Highway-Rail interface was studied and recommendations for improved efficiency and safety were made.

The traffic signal controller architecture was developed to help the research team understand the different roles and responsibilities of the components of signal control logic. Figure I-1 shows the key functional packages within the controller architecture. In the center, the Core Logic represents the standard ring-phase-barrier model of a controller. Each phase is constructed from intervals for vehicle and pedestrian indications. The Strategic Control package represents the logic that would is responsible for providing strategic control such as coordination, preemption, and priority. The Priority Request Generator represents logic from buses, trains, trucks, snowplows, or other vehicles that might request special service from the intersection. The Tactical Control package utilizes Sensors (detectors – loop, video, or other technologies) to determine when to call phases for service and when to call for extension. Control of oversaturated isolated intersections is primarily an issue in the Tactical Control and Core Logic components in this architecture. Control of networks of oversaturated intersections would include the Strategic Control Package.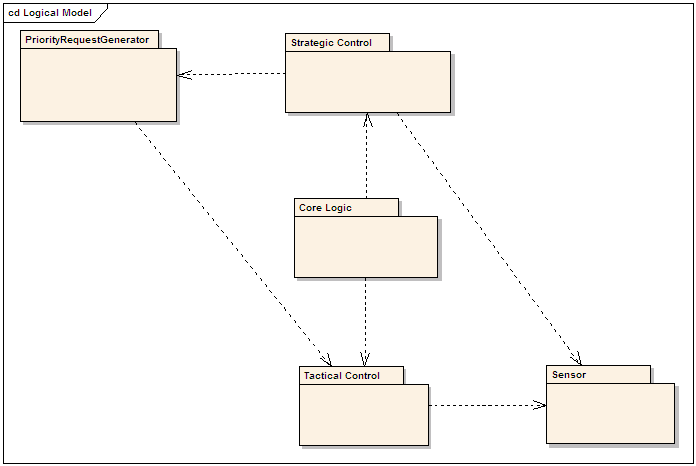

Figure 1-1. Traffic Signal Controller Architecture

A significant effort addressed in the 3-66 research was the Tactical Control logic in terms of how detectors are used to call and extend phases. Several Tactical Control enhancements were investigated including the use of lane-by-lane logic to extend and gap out phases and flow based logic that could request a phase be terminated if the there were vehicles calling a phase, but the vehicles were not flowing due to some obstruction – such as downstream congestion or a blocked lane. These improvements in the Tactical Control logic improve the utilization of green time at the intersection significantly and will be important to the both short term and long term strategies for control of oversaturated intersections.

The 3-66 contributions to the Highway-Rail interface investigated Sensor issues related to track circuits to determine how far in advance a Request for Service could reliably be made to allow safer and smoother preparation for the required Simultaneous Preemption Call. The Core Logic model was used as the foundation for advanced preemption service using concepts from project scheduling to determine which phase intervals could be served, such as pedestrian walk and flashing don't walk and phase extension intervals, and still satisfy the Simultaneous Preemption Call.

The 3-66 research provides a logic framework for consideration of strategies and algorithms for control of oversaturated intersection. The controller architecture helps allocate functionality to the detection and tactical decision making components and to the phase control logic. The Core Logic model provides a decision framework for servicing phases intelligently under oversaturated conditions. The Tactical Control package provides the necessary interface and relationship for future extensions to arterials and networks.

Key findings related to oversaturated control from the 3-66 research primarily include tactical control and sensors; however, the structure of the overall architecture was designed to support analysis of all levels of control and are directly applicable to oversaturated control.

The role of sensors in traffic control is to provide information about the state of traffic demand for service by the shared capacity that is controlled by a traffic signal. Today, most sensors provide tactical input as pulses or present as vehicles cross a defined point in one or more lanes. For example, a stop bar detector can cover multiple lanes on an approach to an intersection and provides a CALL signal to the tactical control level of the controller. The CALL may be active as long as there are vehicles on the approach or may be LOCKED (during the yellow change or red clearance intervals) and cleared when any green (service) interval serves. An upstream passage detector may send a pulse signal to the tactical control unit that may be used to extend a phase if it is during the extension interval or to CALL a phase during the red interval.

The NCHRP 3-66 research addressed two improved roles for sensors including lane-by-lane detection and flow based measurement at the tactical level and a role for sensors in the strategic level including the estimation of volume to capacity (v/c) ratios that are used in the development of signal timing. The idea behind lane-by-lane detection is to address the issues related to lane utilization where one, or more, lanes may be more heavily utilized rather than an equal utilization across all lanes. The lane-by-lane concept also addresses the efficiency of utilization of green time by allowing each lane to "gap out" instead of allowing a ping-pong effect of extension calls in each lane to fully extend the green phase to the maximum green time, yet actually only serving a fraction of the service capacity. Figure I-2 (adopted from the NCHRP 3-66 Final Report) shows this effect. This concept is applicable more in the undersaturated conditions than oversaturated conditions, but is relevant during periods leading to and from oversaturation.

Figure 1-2. Ping-pong effect of lane utilization in traditional detection

Flow based sensors would provide information about the number of vehicles that cross the detector. The concept is based on the use of stop bar detectors to measure flow during the green service interval and the request to terminate green if there is presence but no flow. For example, assume that the downstream link is congested and a movement (e.g. left turn) cannot discharge any vehicles. Traditional control would allow the phase to extend to the maximum green time despite the fact that no vehicles are departing and the green time might be used for another movement. The NCHRP 3-66 research showed that in this condition, the green could be terminated and control could move onto other phases. This might reduce the overall cycle time, hence increasing the frequency of phase service while reducing the duration of service with the effect of increasing the true phase green utilization as measured by flow of vehicles during the green interval. Coordinated operations might constrain this effect by moving the additional green time to the coordinated phase(s) hence reducing the duration, but not increasing the frequency of service. This issue was not addressed by the NCHRP 3-66 project.

The role of sensors in strategic control studies in the NCHRP 3-66 research included the dynamic reallocation of phase split times (green times) based on the measurement of volume to capacity (v/c) ratios. This role addresses the fundamental issue of how traffic signal timings are developed. Currently, a traffic study is conducted where traffic counts (volume and turning counts) are collected on a network over a period of several days. Typically this is done manually, however there are some new tools for automated data collection that are used. These count represent point estimates of the demand for different movements that are used in signal timing software (such as Synchro, TRANSYT, PASSER, etc.) to develop the timings. These point estimates fail to capture the random variations that can occur over time, or on a daily basis and the changes that occur over longer time periods such as weeks, months, or years. The ability to measure and utilize flow data at the intersection could allow the strategic level to reallocate green time to address these variations. Again, this analysis did not address the oversaturated conditions and strategies that could be used to detect (such as phase failures) or address oversaturated phases.

In addition to the NCHRP 3-66 research, Abbas, et.al. looked at the use of system detector data (defined as lane-by-lane volume and occupancy data collected over a one minute of one cycle period at upstream detectors) to evaluate the effectiveness of offsets between intersections. Essentially if the volume was high and the occupancy was low then the offset must be allowing the vehicles to progress through the intersection. If the volume was low and the occupancy is high, then the offset may not be allowing the progression of vehicles and contributing to potential oversaturated conditions.

The core logic model developed in the NCHRP 3-66 research provides an analytical structure for understanding and analyzing the capability of the traffic signal controller. Head, et. al. (2007) represent this model as a precedence graph that is similar to the activity diagram used in project management and critical path analysis. Figure I-3 shows an example of the precedence graph model.

Figure 1-3. Precedence graph model for T-intersection (from Head, et. al. 2007)

This model shows how intervals, such as pedestrian intervals, can constrain the early termination of a phase – as might be requested by the tactical level when there is low or no flow across and stop bar detector. It also helps to show how one phase, or phase group such as phases 1 and 2 in ring 1, may constrain the termination of other phases such as phases 3 and 4 in ring 2. As various tactical and strategic controls are evaluated the interaction and effect of the structural issues are captured in the model. The model is descriptive of controller behavior and not prescriptive of how the controller should operate in oversaturated or undersaturated conditions.

References for NCHRP 3-66 Discussion

Abbas, M., Bullock, D., Head, L, "Real-Time Offset Transitioning Algorithm for Coordinating Traffic Signals", Transportation Research Record No. 1748, TRB, National Research Council, Washington, DC, 2001.

Head, K.L., D.G. Gettman, D. Bullock, and T. Urbanik, "Modeling Traffic Signal Operations Using Precedence Graphs", to appear, Transportation Research Record, TRB, National Research Council, Washington, DC, 2007.

Head, K.L., D. Gettman, and Z. Wei, "A Decision Model For Priority Control of Traffic Signals", Transportation Research Record No. 1978, TRB, National Research Council, Washington, DC, 2006, , pp. 169-177.

Smaglik, E., Bullock, D., Sturdevant, .J, Urbanik, T., "Implementation of Lane-By-Lane Detection at Actuated Controlled Intersection", to appear, Transportation Research Record, TRB, National Research Council, Washington, DC, 2007.