2019 VERSION: Volume III: Guidelines for Applying Traffic Microsimulation Modeling Software 2019 Update to the 2004 Version

2004 Version - Appendix E: Hypothesis Testing of Alternatives

When the microsimulation model is run several times for each alternative, the analyst may find that the variance in the results for each alternative is close to the difference in the mean results for each alternative. How is the analyst to determine if the alternatives are significantly different? To what degree of confidence can the analyst claim that the observed differences in the simulation results are caused by the differences in the alternatives and not just the result of using different random number seeds? This is the purpose of statistical hypothesis testing. Hypothesis testing determines if the analyst has performed an adequate number of repetitions for each alternative to tell the alternatives apart at the analyst's desired level of confidence.

E.1 Estimation of the Required Number of Model Repetitions

This section identifies how to estimate the minimum number of model run repetitions that would be required to determine if two alternatives with results a given distance apart are significantly different. This estimate, however, requires a preliminary estimate of the standard deviation of the model run results for the alternatives, which, in turn, require some preliminary runs to estimate the standard deviation.

The procedure involves the following steps:

1. Perform a preliminary set of model run repetitions for each alternative.
2. Estimate the standard deviation and the mean difference between the alternatives from the preliminary runs and then compute the required number of runs using the equations in this subsection.
3. If the required number of runs is greater than the preliminary number of runs, the analyst should perform the additional repetitions for each alternative and recompute the mean difference and standard deviation using the augmented set of model run repetitions.

E.1.1 Estimation of Pooled Standard Deviation

The analyst should perform about six to eight model repetitions of each alternative to estimate the pooled standard deviation for all alternatives according to the following equation:

 (Equation 16)

where:

s_x = standard deviation of model run results for alternative x

s_y = standard deviation of model run results for alternative y

The preliminary model repetitions used to estimate the pooled estimate of the standard deviation of the model run results can also be used to estimate the likely difference of the means for each alternative.

E.1.2 Selection of Desired Confidence Level

A 95-percent confidence level is often selected for hypothesis testing. This means that there is a 5-percent chance (often called "alpha" in the textbooks) that the analyst will mistakenly reject the null hypothesis when it is really true (type I error). If a higher confidence level is desirable, it comes at the cost of increasing the likelihood of making a type II error (accepting the null hypothesis when it is really false) (Table 9).

Table 9. Null hypothesis.

The study objective may determine the desired confidence level. For example, if the objective is to design an alternative with a 95-percent probability that it will provide significant improvements over the current facility, then this is the appropriate confidence level for the determination of the number of model repetitions required.

E.1.3 Selection of Minimal Difference in the Means

The likely minimal difference in the means between the alternatives should be identified by the analyst. This is the target sensitivity of the simulation tests of the alternatives. Alternatives with mean results farther apart than this minimal difference will obviously be different. Alternatives with mean results closer together than this minimal difference will be considered to be indistinguishable.

The study objectives have some bearing on the selection of the minimal difference to be detected by the simulation tests. If the study objective is to design a highway improvement that reduces mean delay by at least 10 percent, then the tests should be designed to detect if the alternatives are at least 10 percent apart.

The preliminary model repetitions used to estimate the pooled estimate of the standard deviation of the model run results can also be used to estimate the likely difference of the means for each alternative. The smallest observed difference in these preliminary runs would be the selected minimal difference of the means to be used in determining the required number of repetitions.

E.1.4 Computation of Minimum Repetitions

Assuming that the analyst wishes to reject the null hypothesis that the means of the two most similar alternatives are equal with only an alpha percent chance of error against the counter hypothesis that the mean of alternative x is different than y, then the number of repetitions required can be computed according to the following equation:⁷⁰

 (Equation 17)

where:

absolute value of the estimated difference between the mean values for the two most similar alternatives x and y

s_p = pooled estimate of the standard deviation of the model run results for each alternative

n = number of model repetitions required for each alternative

t = t statistic for a confidence level of 1-alpha and 2n-2 degrees of freedom⁷¹

Note that when solving this equation for N, it is necessary to iterate until the estimated number of repetitions matches the number of repetitions assumed when looking up the t statistic. Table 10 provides solutions for this equation for various target mean difference ranges and levels of confidence.

Table 10. Minimum repetitions for distinguishing alternatives.

Notes:

1. The minimum difference in the means is expressed in units of the pooled standard deviation: .

2. For example, if the pooled standard deviation in the delay for two alternatives is 1.5 s, and the desired minimum detectable difference in the means is a 3.0-s delay at a 95-percent confidence level, then it will take four repetitions of each alternative to reject the hypothesis that the observed differences in the simulation results for the two alternatives could be the result of random chance.

E.2 Hypothesis Testing for Two Alternatives

To determine whether simulation output provides sufficient evidence that one alternative is better than the other (e.g., build project versus no-build), it is necessary to perform a statistical hypothesis test of the difference of the mean results for each alternative. A null hypothesis is specified: "The model-predicted difference in VHT for the two alternatives occurred by random chance. There really is no significant difference in the mean travel time between the alternatives." A statistic is computed for a selected level of confidence, and if the difference between the two means is less than that statistic, then the null hypothesis is accepted and it is concluded that there is insufficient evidence to prove that the one alternative is better than the other. The analyst either makes more model repetitions for each alternative (to improve the sensitivity of the test) or relaxes his or her standards (confidence level) for rejecting the null hypothesis.

The specification of the problem is:

Null Hypothesis:

 (Equation 18)

against

 (Equation 19)

where:

µ_x = mean VHT (or some other measure) for alternative x

µ_y = mean for alternative y

This is a two-sided t-test with the following optimal rejection region for a given alpha (acceptable type I error):

 (Equation 20)

where:

absolute value of the difference in the mean results for alternative x and alternative y

s_p = pooled standard deviation

t = Student's t-distribution for a level of confidence of 1-alpha and n+m-2 degrees of freedom

n = sample size for alternative x

m = sample size for alternative y

 (Equation 21)

where:

s_p = pooled standard deviation

s_x = standard deviation of the results for alternative x

s_y = standard deviation of the results for alternative y

n = sample size for alternative x

m = sample size for alternative y

The probability of mistakenly accepting the null hypothesis is alpha (usually set to 5 percent to get a 95-percent confidence level test). This is a type I error.

There is also a chance of mistakenly rejecting the null hypothesis. This is called a type II error and it varies with the difference between the sample means, their standard deviation, and the sample size.⁷²

E.3 Hypothesis Testing for Multiple Alternatives

When performing hypothesis testing on more than one pair of alternatives, it is most efficient to first determine if any of the alternatives are significantly different from the others. An analysis of variance (ANOVA) test is performed to determine if the mean results for any of the alternatives are significantly different from the others:

• If the answer is yes, the analyst goes on to test specific pairs of alternatives.
• If the answer is no, the analysis is complete, or the analyst runs more model repetitions for each alternative to improve the ability of the ANOVA test to discriminate among the alternatives.

E.3.1 Analysis of Variance (ANOVA) Test

The ANOVA test has three basic requirements:

• Independence of samples (random samples).
• Normal sampling distribution of means.
• Equal variances of groups.

Levine's test of heteroscedasticity can be used for testing whether or not the variances of the model run results for each alternative are similar. Less powerful nonparametric tests, such as the Kruskal-Wallis test (K-W statistic) can be performed if the requirements of the ANOVA test cannot be met.

However, the ANOVA test is tolerant of modest violations of these requirements and may still be a useful test under these conditions. The ANOVA test will tend to be conservative if its requirements are not completely met (less likely to have a type I error with a lower power of the test to correctly reject the null hypothesis).

To perform the ANOVA test, first compute the test statistic:

 (Equation 22)

where:

F = test statistic

MSB = mean square error between the alternatives (formula provided below)

MSW = mean square error among the model results for the same alternative (within alternatives)

The formulas below show how to compute MSB and MSW:

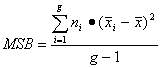 (Equation 23)

where:

MSB = mean square error between the alternatives (i = 1 to g)

n_i = number of model runs with different random number seeds for alternative i

mean value for alternative i

mean value averaged across all alternatives and runs

g = number of alternatives

and

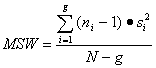 (Equation 24)

where:

MSB = mean square error between the alternatives (i = 1 to g)

n_i = number of model runs with different random number seeds for alternative i

variance of the model run results for alternative i

N = total number of model runs summed over all alternatives

g = number of alternatives

The null hypothesis of equal means is rejected if:

F > F_{1-alpha,g-1,N-g} (Equation 25)

where:

F_{1-alpha,g-1,N-g} = F statistic for a type I error of alpha (alpha is usually set at 5 percent for a 95-percent confidence level) and g-1 and N-g degrees of freedom. N is the total number of model runs summed over all alternatives; g is the number of alternatives

If the null hypothesis cannot be rejected, then the analysis is either complete (there is no statistically significant difference between any of the alternatives at the 95-percent confidence level) or the analyst should consider reducing the level of confidence to below 95 percent or implementing more model runs per alternative to improve the sensitivity of the ANOVA test.

E.3.2 Pairwise Tests of Some Pairs of Alternatives

If performing hypothesis tests for only a few of the potential pairs of alternatives, the standard t-test can be used for comparing a single pair of alternatives:

 (Equation 26)

absolute value of the difference in the mean results for alternative x and alternative y

s_p = pooled standard deviation

t = t distribution for a level of confidence of 1-alpha and n+m-2 degrees of freedom

n = sample size for alternative x

m = sample size for alternative y

 (Equation 27)

where:

s_p = pooled standard deviation

s_x = standard deviation of the results for alternative x

s_y = standard deviation of the results for alternative y

n = sample size for alternative x

m = sample size for alternative y

If one merely wishes to test that the best alternative is truly superior to the next best alternative, then the test needs to be performed only once.

If one wishes to test other possible pairs of alternatives (such as second best versus third best), it is possible to still use the same t-test; however, the analyst should be cautioned that the level of confidence diminishes each time the test is actually performed (even if the analyst retains the same nominal 95-percent confidence level in the computation, the mere fact of repeating the computation reduces its confidence level). For example, a 95-percent confidence level test repeated twice would have a net confidence level for both tests of (0.95)², or 90 percent.

Some experts, however, have argued that the standard t-test is still appropriate for multiple paired tests, even at its reduced confidence level.

E.3.3 Pairwise Tests of All Pairs of Alternatives

To preserve a high confidence level for all possible paired tests of alternatives, the more conservative John Tukey "Honestly Significantly Different" (HSD) test should be used to determine if the null hypothesis (that the two means are equal) can be rejected.⁷³

The critical statistic is:

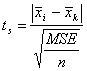 (Equation 28)

where:

t_s = Studentized t-statistic

mean value for alternative i

MSE = mean square error = MSB + MSW

N = number of model runs with different random number seeds for each alternative (if the number of runs for each alternative is different, then use the harmonic mean of the number of runs for each alternative)

Reject the null hypothesis that the mean result for alternative i is equal to that for alternative k if:

t_s > t_1-alpha,g-1 (Equation 29)

where:

t_1-alpha,g-1 = t statistic for a desired type I error of alpha (alpha is usually set at 5 percent to obtain a 95-percent confidence level) and g-1 degrees of freedom, with g equal to the total number of alternatives tested, not just the two being compared in each test.

Some experts consider the HSD test to be too conservative, failing to reject the null hypothesis of equal means when it should be rejected. The price of retaining a high confidence level (the same as retaining a low probability of a type I error) is a significantly increased probability of making a type II error (accepting the null hypothesis when it is really false).

E.4 What To Do If the Null Hypothesis Cannot Be Rejected

If the null hypothesis of no significant difference in the mean results for the alternatives cannot be rejected, then the analyst has the following options:

• Increase the number of model run repetitions per alternative until the simulation performance of one alternative can be distinguished from the other.
• Reduce the confidence level from 95 percent to a lower level where the two alternatives are significantly different and report the lower confidence level in the results.
• Accept the result that the two alternatives are not significantly different.