|
|
|
This section explains how to compute the confidence intervals for the microsimulation model results. It explains how to compute the minimum number of repeated field measurements or microsimulation model runs needed to estimate the mean with a certain level of confidence that the true mean actually falls within a target interval.
Three pieces of information are required: (1) sample standard deviation, (2) desired length of the confidence interval, and (3) desired level of confidence.
The required number of repetitions must be estimated by an iterative process. A preliminary set of repetitions is usually required to make the first estimate of the standard deviation for the results. The first estimate of the standard deviation is then used to estimate the number of repetitions required to make statistical conclusions about alternative highway improvements.
When all of the repetitions have been completed, the analyst then recomputes the standard deviation and the required number of repetitions based on all of the completed repetitions. If the required number of repetitions is less than or equal to the completed number of repetitions, then the analysis has been completed. If not, the analyst either relaxes the desired degree of confidence in the results or performs additional repetitions.
Multiple repetitions of the same model are required because microsimulation results will vary depending on the random number seed used in each run. The random number seed is used to select a sequence of random numbers that are used to make numerous decisions throughout the simulation run (Should a vehicle be loaded on the network now or later? Should the driver be aggressive or timid? Which vehicle type should it be? Will the driver choose the shortest path or a slightly longer one instead?). The outcomes of all of these decisions will affect the simulation results. The results of each run will usually be close to the average of all of the runs; however, each run will be different from the other.
Figure 14 shows the range of results that can occur simply by varying the random number seed used in each run. The figure shows the mean system vehicle speed for a freeway-to-freeway interchange during each minute of the simulation run. A total of six simulation runs (called "processes" in the figure) were made. As can be seen, after the initial warmup period, results diverge. The range of mean speeds output by each process is about 8.1 to 9.7 km/h (5 to 6 mi/h) for most of the length of the simulation period. Running a longer simulation period does not reduce this variation. At the end of the simulation, the range of results is about 9.7 km/h (6 mi/h), or 25 percent of the mean system speed at the end of the simulation period.
Source: I-580/I-680 Freeway Interchange Model, Dowling Associates, 2002
Note: Metric conversion: 1 mi/h = 1.61 km/h
The standard deviation (an estimate of the variance) is required to estimate the number of repetitions. However, it takes a minimum number of repetitions to estimate the standard deviation in the first place. So either the analyst estimates the standard deviation directly (based on past experience) or executes a few model run repetitions (each run using a different random number seed) and uses the equation below to compute an initial estimate of the sample standard deviation.
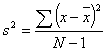(Equation 12)
where:
s = standard deviation
x = variable (such as delay) for which the sample variance is desired
= average value of the variable produced by the model runs
N = number of model runs
Unless the analyst already knows the standard deviation from experience, it is recommended that four repetitions be performed for the initial estimation of the standard deviation. This initial estimate is then revisited and revised later if and when additional repetitions are performed for the purposes of obtaining more precise estimates of mean values or for alternatives analysis.
The confidence level is the probability that the true mean lies within the target confidence interval. The analyst must decide to what degree he or she wishes to know the interval in which the true mean value lies. The usual approach is to pick a 95-percent level of confidence; however, analysts may choose higher or lower levels of confidence. Higher levels of confidence require more repetitions.
The confidence interval is the range of values within which the true mean value may lie. The length of the interval is at the discretion of the analyst and may vary according to the purposes for which the results will be used. For example, if the analyst is testing alternatives that are very similar, then a very small confidence interval will be desirable to distinguish between the alternatives. If the analyst is testing alternatives with greater differences, then a larger confidence interval can be tolerated. Smaller confidence intervals require more repetitions to achieve a given level of confidence. Confidence intervals that are less than half the value of the standard deviation will require a large number of repetitions to achieve reasonable confidence levels.67
It is impossible to know in advance exactly how many model runs will be needed to determine a mean (or any other statistical value) to the analyst's satisfaction. However, after a few model runs, the analyst can make an estimate of how many more runs may be required to obtain a statistically valid result.
The required minimum number of model repetitions is computed using the following equation:
(Equation 13)
where:
CI(1-alpha)% = (1-alpha)% confidence interval for the true mean, where alpha equals the probability of the true mean not lying within the confidence interval
t(1-alpha/2),N-1 = Student's t-statistic for the probability of a two-sided error summing to alpha with N-1 degrees of freedom, where N equals the number of repetitions
s = standard deviation of the model results
Note that when solving this equation for N, it will be necessary to iterate until the estimated number of repetitions matches the number of repetitions assumed when looking up the t statistic. Table 8 shows the solutions to the above equation in terms of the minimum number of repetitions for various desired confidence intervals and desired degrees of confidence.
Desired Range (CI/S) |
Desired Confidence |
Minimum Repetitions |
|---|---|---|
0.5 |
99% |
130 |
0.5 |
95% |
83 |
0.5 |
90% |
64 |
1.0 |
99% |
36 |
1.0 |
95% |
23 |
1.0 |
90% |
18 |
1.5 |
99% |
18 |
1.5 |
95% |
12 |
1.5 |
90% |
9 |
2.0 |
99% |
12 |
2.0 |
95% |
8 |
2.0 |
90% |
6 |
Notes:
1. Desired Range = desired confidence interval (CI) divided by standard deviation (S)
2. For example, if the standard deviation in the delay is 1.5 s and the desired confidence interval is 3.0 s at a 95-percent confidence level, then it will take eight repetitions to estimate the mean delay to within ± 1.5 s.
Table of Contents | List of Tables | List of Figures | Top of Section | Previous Section | Next Section | HOME
