Approaches to Forecasting the Third Performance Management Rulemaking (PM3) Measures for Target Setting

Chapter 4. Model-Based Forecasts of Targets

As opposed to the previous methods identified, forecasting performance represents a mid- to long-term challenge that DOTs and local agencies must confront in order to transition from a performance measurement to a performance management approach. For mobility measures, while travel demand models (TDM) forecast performance measures such as volume-to-capacity (v/c) and vehicle-hours traveled, TDMs do not forecast any of the PM3 reliability or delay measures. A target setting approach utilizing such a tool would have the advantages of 1) being able to incorporate the effects of external factors that affect performance and are beyond a State DOT’s or MPO’s control or influence; and 2) accounting for the effects of improvements on progress towards targets.

A potential approach for forecasting mid and long-range mobility and PM3 performance measures is to adapt the reliability forecasting methods and tools developed under the Strategic Highway Research Program 2 (SHRP 2). While these tools were not explicitly designed to support target setting, they can be adapted for that use. Table 4 shows the SHRP 2 reliability tools that could be adapted to forecasting the PM3 measures. While several of the procedures can calculate the required metrics for system and truck reliability (50^th, 80^th, and 95^th percentile travel times), they would have to be produced for the multiple hours and day of week that comprise the time periods required. Therefore, in the sections below we present a hypothetical approach to forecasting the PM3 measures based on TDM output for a corridor. An issue that arises is that the links in the TDM network do not necessarily correspond to TMC segments, and they would have to be conflated with empirical data are to be used. Such a hybrid model—combining empirical data with forecasted demand—could be a powerful tool for predicting performance. For the purpose of demonstrating the method, though, we assume that empirical travel time data is not available.

Table 4. Strategic Highway Research Program 2 reliability tools.¹⁶

Strategic Highway Research Program 2 Project	Analysis Scale (in order of increasing complexity)
L03 and C11	Sketch planning; system or project level.
L07	Detailed sketch planning; mainly project level.
L02	Performance monitoring and project evaluations using empirical data.
L10	Performance monitoring and project evaluations using empirical data.
L08	Project planning using Highway Capacity Manual scale of analysis.
C05	Project planning using mesoscopic simulation scale of analysis.
C10	Regional planning using linked travel demand and mesoscopic simulation analysis.
L04	Regional planning using linked travel demand and mesoscopic or microscopic simulation analysis.

Data Requirements

We assume that the TDM forecasts traffic by the following time periods (weekday):

• AM Peak: 6:00 a.m.–9:00 a.m.
• Mid-day: 9:00 a.m.–4:00 p.m.
• PM Peak: 4:00 p.m.–7:00 p.m.
• Overnight: 7:00 p.m.–6:00 a.m.

Beyond the data requirements operating the TDM, data on hourly traffic distributions are required. These are required to split out the link volume forecasts into hours. Because most links in a TDM network are one way, the distributions need to be by direction, where direction is travel direction that peaks in either the morning or afternoon on weekdays. Links can be assigned to a “peaking direction” by examining speeds or v/c ratios; the AM or PM period with the highest value will indicate the peaking direction.

Table 5 shows an example of these hourly distributions. Because the System and Truck Reliability measures also consider weekend time periods, distributions for weekends also are required. Factors to compute annual average weekday traffic (AAWDT) and annual average weekend traffic (AAWET) also are needed.

TDMs predict single values for their performance measures meant to represent the average or typical condition. However, the System and Truck Reliability measures are based on the variability around this average condition. Therefore, some method of translating the average condition into the travel time percentiles for the performance metrics needs to be developed. The tactic used by SHRP 2 Project C11, where empirical data is used to develop relationships between the average condition and the percentiles can be used for this purpose. Figure 4 shows an example of this relationship developed from the NPMRDS data for Oregon. Note that the travel time index is used for this relationship in order to normalize the data for different section lengths.

Table 5. Example traffic distributions.

Hour	Weekday AM Peak Direction—Percent of Daily Traffic	Weekday PM Peak Direction—Percent of Daily Traffic	Weekend (both directions)—Percent of Daily Traffic
0	0.42	0.58	2.16
1	0.27	0.33	1.45
2	0.23	0.25	1.06
3	0.23	0.22	0.69
4	0.38	0.29	0.63
5	1.17	0.68	1.02
6	3.26	1.75	1.98
7	4.83	2.9	2.87
8	3.56	2.57	3.70
9	2.58	2.24	4.69
10	2.46	2.33	5.66
11	2.56	2.56	6.45
12	2.65	2.71	7.06
13	2.7	2.77	7.06
14	2.93	3.12	7.09
15	3.26	4.01	7.19
16	3.47	4.81	7.19
17	3.42	4.85	6.90
18	2.66	3.23	6.22
19	1.95	2.23	5.15
20	1.54	1.78	4.24
21	1.4	1.63	3.77
22	1.14	1.3	3.27
23	0.79	0.98	2.50

Analysis Tools

In addition to the TDM, code will have to be developed to perform the processing steps below. Spreadsheets are probably not adequate.

Figure 4. Chart. Empirical relationship for predicting the 80^th percentile Travel Time Index.

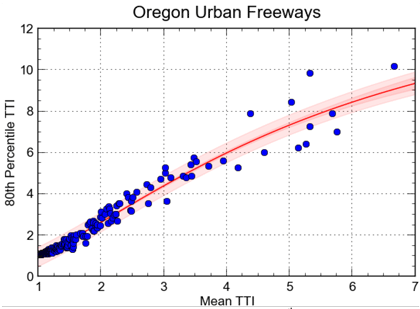
Source: FHWA.

Forecasting Measures and Target Setting Process

The approach to developing the PM3 measures from TDM output involves the following processing steps:

1. Obtain the following link-level information from the output of the TDM:
   • Free-flow speed.
   • Number of lanes.
   • Assigned volumes for each time period.
   • Link capacity for each time period. The link capacity should correspond to the capacity as defined by the Highway Capacity Manual.¹⁷
2. Develop hourly volumes for weekdays and weekends:
   • Sum the assigned volumes over all time periods to calculate AAWDT. Apply the hourly distributions to get weekday volumes by hour.
   • Repeat the process for weekend volumes, except that AAWDT must be converted to AAWET, which is usually lower, before applying the weekend hourly distributions.
3. Compute v/c ratios by hour.
4. Use a volume-delay function (VDF) to compute the travel time on the link. While TDM models also use a VDF as part of the traffic assignment process, it is applied for the entire period, not individual hours. The Bureau of Public Roads (BPR) function is a traditional VDF but many more exist. The BPR formulation is:

   Figure 5. Equation. Predicted travel time on the link.

   

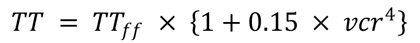
   Source: FHWA.

   Where:

   TT = the predicted travel time on the link
   TT_ff = the travel time at the free-flow speed
   vcr = the v/c ratio

5. Compute the travel time for each hour in the LOTTR and TTTR time periods by link. Compute the metrics for the PHED delay measure as well.
6. Compute the average travel time for each LOTTR and TTTR time period by link, then the mean travel time index (MTTI) as the average travel time divided by the free-flow travel time.
7. Compute the 50^th, 80^th, and 95^th percentile travel times as a function of MTTI from the empirical relationships. From this point on, use the same calculation procedures for the system and truck reliability measures and the PHED measure as those used with empirical data.

The above procedure is a simplistic approach to the problem because the volumes and capacities used are static; since reliability is defined by how travel times vary, then its determinants also should vary. Two methods exist to extend the procedure to include variability in demand (volumes) and capacity.

The simplest adjustment is to increase the v/c ratio to account for increased demand and/or decreased capacity due to disruptions such as incidents and inclement weather. However, the development of the v/c adjustments must account for the fact that incidents and weather occur with variable severities, e.g., incidents do not occur every day on a highway section and when they do, their blockage and duration characteristics vary.) From a prediction standpoint, in addition to being probabilistic, incidents also are a function of VMT, so care must be taken in reducing capacity in the v/c ratio.

A second more complex method is to compute travel times stochastically. In this approach, the volume and capacity on a link are allowed to vary using Monte Carlo simulation techniques, and travel times for each level of volume and capacity are computed until a complete travel time distribution is obtained. Distributions for the factors being varied are required for the Monte Carlo simulation. The resulting synthetic distribution of travel times can then be used in the same way that empirical data are used for computing the PM3 measures. The procedure works as follows for incidents, but weather and volumes also can be addressed: The idea is to cycle through individual “days” where each day has distinct incident characteristics:

• Determine if an incident occurs during this hour by sampling from a Poisson distribution, where the lambda parameter is the VMT times the incident rate.
• Determine the blockage characteristics: shoulder or the number of lanes blocked by sampling from the incident blockage distribution.
• Reduce capacity to account for the incident blockage. The Highway Capacity Manual has information for capacity reduction factors due to incidents.
• Apply the VDF and store the travel time.
• Repeat over multiple “days” (replications) to create the travel time distribution.

Weather conditions can also be sampled using the above approach. Thus, each simulated “day” is a combination of incident and weather conditions.

Example

An MPO wants to develop the PM3 measures for their region as part of their Long-Range Transportation Plan (LRTP). They have run their Travel Demand Forecasting (TDF) model for multiple scenarios and have developed code to process the TDF model output to develop the measures. The calculations follow the process below shown for a single freeway link one mile in length and three lanes wide for the first time period for the System Reliability measure:

• The free-flow speed is 60 mph and the link has a calculated capacity of 2,200 passenger cars per hour per lane (pcphpl). To account for the effect of disruptions, the net effect is to reduce capacity by 10 percent, bringing the revised capacity to 1,980 pcphpl.
• One-way AAWDT for the link has been computed as 50,000 from the model output. Using a local hourly traffic distribution, the volume in each hour is determined:
  • 6:00 a.m.–7:00 a.m.: 4,800 vehicles per hour.
  • 7:00 a.m.–8:00 a.m.: 5,700 vehicles per hour.
  • 8:00 a.m.–9:00 a.m.: 5,200 vehicles per hour.
• The v/c ratios are calculated and the BPR VDF is used to compute the average travel times. Corresponding speeds and MTTIs also are computed (table 6).
• For the entire 6:00 a.m.–9:00 a.m. time period, the volume-weighted average travel time is computed as 1.095 minutes. The MTTI also is 1.095 (given that the link is 1 mile long and the free-flow speed is 60 mph).
• Using locally derived relationships similar to the one shown in figure 4:
  • 50^th percentile travel time index (TTI) is 1.070.
  • 80^th percentile TTI is 1.138.
  • 95^th percentile TTI is 1.225.
• The LOTTR metric for this link and time period is 1.138/1.070 = 1.063.
• LOTTR metrics for all time periods and links are computed in the same manner as for empirical data. The System Reliability measure is then computed.

Table 6. Link calculations.

Time Period	Volume	Volume-to-Capacity	Travel Time (minutes)	Speed	Travel Time Index
6:00 a.m.–7:00 a.m.	4,800	0.808	1.064	56.4	1.064
7:00 a.m.–8:00 a.m.	5,700	0.960	1.127	53.2	1.127
8:00 a.m.–9:00 a.m.	5,200	0.875	1.088	55.1	1.088