3.3 BCA when Marginal-Cost Pricing Is More the Exception than the Rule
In Section 3.2, we dealt with a world in which marginal-cost prices prevail not just in private markets but also for using of facilities provided by governmental agencies. In that world, we attempted to show all the benefits that an improved road provides to producers and consumers who directly or indirectly benefit from the road improvement could be measured from user demand schedules for just the improved road—if only we could measure them.
Alas, marginal-cost prices are much more the exception than the rule in the real world's economies. If marginal-cost prices are not charged for road services, determining the net benefits of a road improvement requires analysis of the use not just of the improved road itself but also of all other roads with traffic patterns that are affected by those on the improved road.
What's more, most business firms face downward-sloping demand schedules–they can raise their prices a bit without driving all of their customers away. They can lower their prices a bit without being overwhelmed by new patrons. What matters to profit-maximizing business firms in such markets is not just what newly attracted customers pay them but, rather, the additional net revenues the additional customers provide if, as is usually the case, the price reductions that attract new customers must also be provided to customers who are willing to pay higher prices. Profit maximizing firms that face downward-sloping demand schedules try to equate the marginal revenue of additional sales to the marginal cost of those sales. With downward sloping demand schedules, in equilibrium, a marginal gizmo buyer values it at more than it costs Consolidated Gizmo to produce. In turn, sellers' input demand schedules reflect the marginal revenues to which these inputs contribute, not the market values of outputs to which the inputs contribute. Input demand schedules in such markets provide downward-biased estimates of the values of the products to which they contribute. Even if we knew the demand schedules for the services of all roads affected by each road improvement, estimating accurately the benefits associated with these schedules would require us to know details of the underlying cost and demand schedules for products.
In dealing with these issues, we begin with the benefit-measurement problems associated with the absence of marginal-cost road pricing. We then move on to the theoretical problems involved in incorporating elements of monopoly into the benefit-measurement problem. We conclude by discussing how real-world data can contribute to overcoming these estimation problems.
3.3.1 Measuring Aggregate Benefits when Marginal-Cost Tolls Are Not Charged
In the United States, highway user charges normally differ—often by quite substantial amounts—from those required to equate trip prices with their associated marginal costs. As a result, the aggregate benefits derived from highway use are lower than they could be. Also, measuring benefits is considerably less difficult when marginal-cost prices prevail than when they do not. Regardless of the toll level, the benefit a highway improvement gives is the sum of the changes in consumers' surpluses and toll revenues to which it gives rise. However, while surplus and revenue benefits on other than the improved road cancel out when prices equal marginal costs this cancellation does not occur without marginal-cost prices.
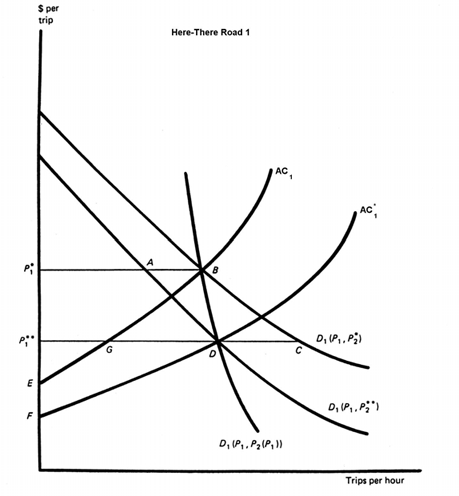
Exhibit 12: Direct and indirect effects of road improvements with zero tolls.
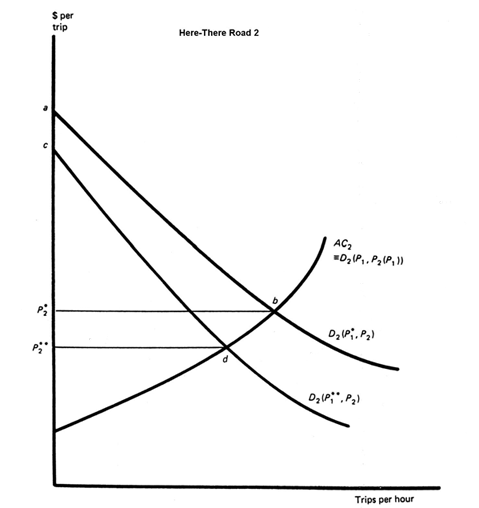
Exhibit 13: Direct and indirect effects of road improvements with zero tolls.
It is worthwhile considering two sorts of situations in which prices differ from marginal costs: first, when no tolls are levied for highway use; second while tolls are charged, they do not equate price and marginal cost. Exhibit 12 deals with the benefit implications of zero user charges. Its interpretation is quite similar to that of Exhibit 8. The basic difference between them is that the upward sloping lines in Exhibit 8 refer to the short-run marginal costs of trips while the corresponding lines in Exhibit 12 are their short-run average costs. That is, the Exhibit 8 lines include but the Exhibit 12 lines exclude the costs users of Roads 1 and 2 users impose on each other by adding to congestion levels.
In the absence of tolls, consumers and carriers incur only travel-time and vehicle-operating costs. The equilibrium travel rate on each road is, therefore, that which the "last" traveler values at its direct costs. Before the improvement, these equilibrium occur at points![]() B and
B and![]() b respectively on Roads 1 and 2. Net consumer benefits on the two roads are therefore areas
b respectively on Roads 1 and 2. Net consumer benefits on the two roads are therefore areas![]() ABP1* and
ABP1* and![]() abP2*. If user charges are not imposed, these consumer benefits are all society gains from using the roads.
abP2*. If user charges are not imposed, these consumer benefits are all society gains from using the roads.
Through a process identical to that discussed in describing Exhibit 8, improving Road 1 would lead to new equilibrium travel rates at points D and d respectively on Roads 1 and 2. As with Exhibit 8, a variety of consumer benefit measures with approximately equal values could be described for the shift from ![]() B and b to
B and b to ![]() D and d. As before, the measure of greatest interest is the sum of
D and d. As before, the measure of greatest interest is the sum of![]() P1*BDP1** on Road 1 and
P1*BDP1** on Road 1 and![]() P2*bdP2** on Road 2. As with Exhibit 8, constructing this benefit measure requires viewing the price of Road 2 trips as a function,
P2*bdP2** on Road 2. As with Exhibit 8, constructing this benefit measure requires viewing the price of Road 2 trips as a function,![]() P2(P1), of the price of Road 1 trips. The resulting demand schedule for Road 1 trips is
P2(P1), of the price of Road 1 trips. The resulting demand schedule for Road 1 trips is![]() D1[P1,P1(P1)], while that for Road 2 trips is superimposed on the average cost schedule for these trips. Unlike the situation with Exhibit 8, however, the benefit to Road 2 road users is a net benefit. Since no tolls are collected, there is no transfer to users of income formerly received by society at large.
D1[P1,P1(P1)], while that for Road 2 trips is superimposed on the average cost schedule for these trips. Unlike the situation with Exhibit 8, however, the benefit to Road 2 road users is a net benefit. Since no tolls are collected, there is no transfer to users of income formerly received by society at large.
To summarize, if trips are not tolled, determining the net short-run benefits of improving one link on a highway system requires information on the effects of that improvement on the use of all other links in the network. Specifically, the benefit equals the sum over all affected links of the changes in consumers' surplus benefits—some of which may be negative—that the improvement induces.
In the United States, the basic "toll" for highway use is that implicit in federal and state gasoline taxes and other excises that are related to the rates at which vehicles are operated. For the use of expressways, these taxes work out to roughly 1 cent per private passenger vehicle mile, regardless of traffic conditions. If the occupants of the average private passenger vehicle value their time at $1.55 an hour, 1 cent per mile is approximately the cost any given expressway trip imposes on other expressway travelers only when the volume-capacity ratio on the expressway is about 50 percent. For a volume-capacity ratio of 90 percent, an expressway toll on the order of 3.7 cents per vehicle mile would be required to equate the price of a trip with its marginal cost, while for a 10 percent volume-capacity ratio, a toll of about 0.1 cents would be appropriate. The corresponding optimum tolls for travel on city streets are 0.4, 2.9, and 11.7 cents for respective volume-capacity ratios of 0.1, 0.5, and 0.9[12].
To repeat, regardless of the toll levels set, an improvement's net benefit equals the sum of the changes in consumers' surplus and toll-revenue benefits to which it gives rise. Measuring net benefits when price and marginal cost are unequal would simply require adding up these changes for all affected highway links with, of course, a heavy computational burden. This computational burden can be reduced somewhat and additional insights into the economic processes involved can be obtained by employing "dead-weight loss" geometry.
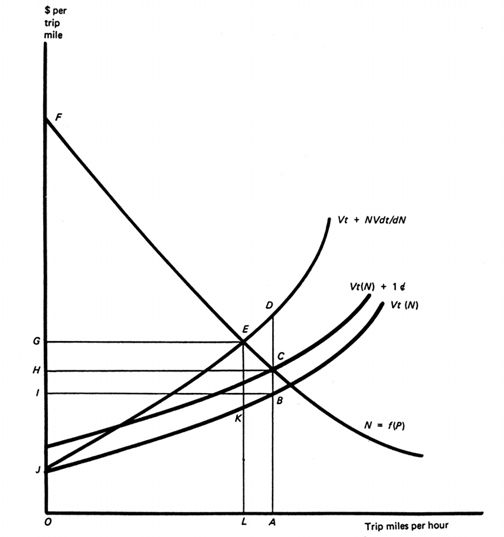
Exhibit 14: Direct benefits of road use with inefficient tolls.
Exhibit 14 describes a single one-mile highway when the marginal-cost toll exceeds that actually charged. With a marginal-cost toll of KE per trip mile, OL trips per hour would be taken. Total hourly benefits of FEJ would result. Of this total, traveler benefits would equal FEG while highway tolls or rents would equal GEJ. However, if a toll of only BC = 1 cent per vehicle mile is charged, OA trips per hour would be taken, this being the travel rate at which the price charged for trips equals the number demanded at that price. With this travel rate, total hourly benefits equal the area FCBI—a traveler benefit of FCH plus tolls of HCBI.
Consumer benefits with the 1-cent toll are GECH greater than those associated with a marginal-cost price. However, these additional consumer benefits are more than offset by the associated reduction in highway rents. Specifically, in going from a marginal-cost toll to a 1-cent toll, the decrease from GEJ to HCBI in rents collected exceeds the increase, GECH, in consumer benefits by an amount equal to area EDC. Put differently, with a 1-cent toll, total short run benefits generated by the highway equal area FEJ minus area EDC.
Area EDC itself can be interpreted as the total short-run costs (area LEDA) of increasing trip consumption from OL to OA minus the total value (area LECA) consumers attach to these addition LA trips. Areas such as EDC are often referred to as "dead-weight losses"—i.e., amounts by which the maximum benefits that could be derived by society from some economic activity are reduced through inefficient pricing.
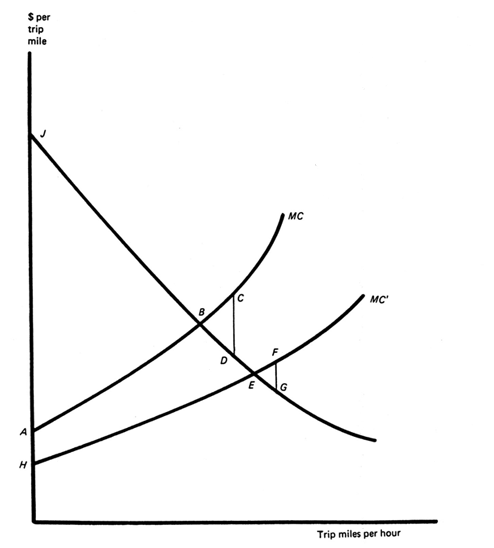
Exhibit 15: Change in dead-weight loss with road improvement.
Suppose that an improvement is made to a highway that is initially priced in the inefficient fashion described in Exhibit 14. As a result, the situation depicted in Exhibit 15 comes about. Even with the improved highway, a 1-cent per mile toll is less than that required to equate demand and marginal-cost schedules. A dead-weight loss is therefore still involved in the highway's pricing. However, the size of the loss has diminished from BDC (equals EDC in Exhibit 3-2 to EFG. The incremental net benefit of the improvement can therefore be viewed as ABEH (the equivalent of, e.g., BDEA in Exhibit 6) plus the difference between BCD and EFD.
To generalize, a given improvement to a highway will lead to a somewhat greater net benefit if its services are initially underpriced than if a marginal-cost price is charged for them. By the same token, however, a given improvement will lead to a smaller net benefit if a highway's services are initially overpriced rather than priced at marginal-cost. That is, if price initially exceeds marginal-cost, an improvement will almost invariably serve to increase the gap between price and marginal cost and thereby the deadweight loss.
At least on urban highways, the user charge implicit in gasoline and related excises seems typically to fall considerably short of the appropriate marginal-cost toll during peak travel periods and to be somewhat greater than marginal cost during other times of day. This being the case, the changes in deadweight losses associated with urban highway improvements tend to offset each other. An improvement can generally be expected to decrease deadweight losses during peak travel hours but to increase them during off-peak hours.
3.3.2 Taking Monopoly Elements into Account in Measuring Aggregate Benefits
The nature of the problem here can be suggested with the aid of a simple diagram, Exhibit 12. Suppose, initially, that the gizmo industry is competitively organized. Each of its members incurs manufacturing and transport costs of OA and AC, respectively, per gizmo. The industry demand schedule intersects its supply/unit-cost schedule at H for a weekly output of OY. At this output rate, gizmo buyers receive a weekly consumers' surplus benefit of LHC while gizmo manufacturers just break even.
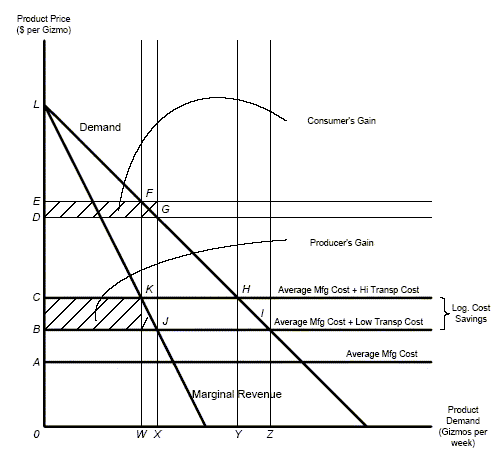
Exhibit 16: Monopoly and benefit allocation.
Suppose, now, that transportation improvements cut gizmo unit transportation costs in half, from AC to AB. After a period of adjustment, industry output expands from OY to OZ per week and the gizmo price falls to OB. The benefit of the improvements to gizmo buyers is area CHIB, the area under the industry's transport demand schedule between prices of OC and OB. As in the previous equilibrium, gizmo consumers reap all benefits from the improvement; after the market fully adjusts to changes in its cost structure, gizmo producers again just break even.
Now suppose that, before the transportation improvement is made, a plutocrat forms Consolidated Gizmo of America to buy out all gizmo producers in the United States. Ignoring the possibility that gizmo price increases would induce new entry to the industry, in the interests of maximizing profits, CGA would reduce its capacity from OY to OW per week, the level at which its marginal-revenue and unit-cost schedules intersect. Its profit-maximizing price is OE. Its customers receive a consumers' surplus benefit of LEF while CGA's profits are twice that, LCK = EFKC.
After the major transport improvement cuts CGA's unit transport costs from AC to AB, its new profit-maximizing output and profit rates are respectively OX and LBJ, an amount that is CKJB greater than its previous profit rate. This is the amount that its transportation demand schedule shows CGA to receive from the improvement. In addition to CGA's gain, however, its customers benefit by EFGD each week. This benefit is not part of CGA's profit increase; true net benefits of the improvement are, therefore, 1.5 times those that would be inferred from CGA's transport demand schedule.
The fraction of the total benefits of a transport improvement that elements of monopoly can hide depends on specifics of the cost and demand schedules that monopolists face. We restrict attention here to markets that are characterized by "Constant elasticities of demand" and to costs that are proportional to sales. The elasticity of demand for a commodity is the percentage change in the quantity sold divided by the percentage change in its price that brought the sales change about. A general expression for a constant-elasticity-of-demand schedule is![]() Q = a/P b where Q is the quantity that would be sold at a price of P and where a and b are constants. It can be shown that b is the elasticity of demand.
Q = a/P b where Q is the quantity that would be sold at a price of P and where a and b are constants. It can be shown that b is the elasticity of demand.
It is possible to show[13] that, given a constant demand elasticity, if P is the current price of gizmos, reducing the price by just enough to sell one more of them would generate![]() (1 − 1/b)P in additional revenues. Note that, if b is less than one,
(1 − 1/b)P in additional revenues. Note that, if b is less than one,![]() (1 − 1/b) is negative; an additional sale would reduce total revenue. A gizmo monopolist would not willingly set its price at a level for which b is less than one.
(1 − 1/b) is negative; an additional sale would reduce total revenue. A gizmo monopolist would not willingly set its price at a level for which b is less than one.
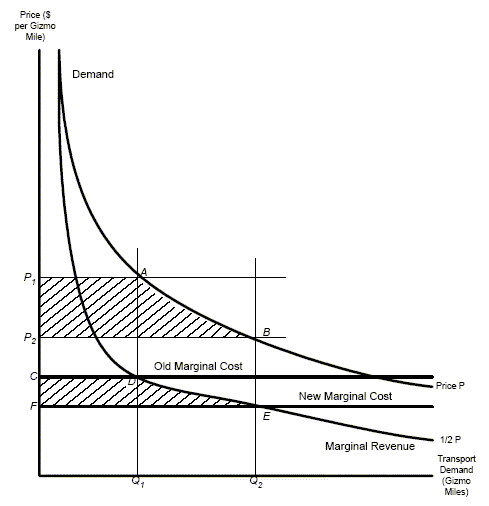
Exhibit 17: Monopoly benefit under-estimation.
Exhibit 17 shows the relationship between price and marginal revenue for a specific instance where the constant elasticity of demand, b, is 2. For this case, marginal revenue at any given price is half that price. Suppose that the marginal cost of producing and delivering a gizmo is OC, along the line labeled "Marginal Cost Old." Marginal revenue equals marginal cost at an output of![]() Q1. Suppose that a reduction in transportation costs–or any other cost, for that matter–reduces production plus distribution costs to "Marginal Cost New." Marginal revenue now equals marginal cost at an output of
Q1. Suppose that a reduction in transportation costs–or any other cost, for that matter–reduces production plus distribution costs to "Marginal Cost New." Marginal revenue now equals marginal cost at an output of![]() OQ2.
OQ2.
Again, in this example, marginal revenue equals the market price divided by two;![]() OC = P1/2 and and
OC = P1/2 and and![]() OF = P2/2. Hence,
OF = P2/2. Hence,![]() OC − OF = (P1 − P2)/2; the transportation improvement results in a price reduction equal to twice that of its reduction in marginal cost. In Exhibit 3-5, CDEF is CGA's benefit from the transport improvement. It is CDEF that we would compute if we observed CGA's transport demand schedule. With a demand elasticity of 2, consumers receive twice the producer's benefit from this cost reduction; the producer's benefit is only a third of the total benefit.
OC − OF = (P1 − P2)/2; the transportation improvement results in a price reduction equal to twice that of its reduction in marginal cost. In Exhibit 3-5, CDEF is CGA's benefit from the transport improvement. It is CDEF that we would compute if we observed CGA's transport demand schedule. With a demand elasticity of 2, consumers receive twice the producer's benefit from this cost reduction; the producer's benefit is only a third of the total benefit.
| Elasticity | Marginal Revenue/Price |
Consumer/Producer Benefit |
|---|---|---|
| 1.5 | 0.33 | 3.00 |
| 2.0 | 0.50 | 2.00 |
| 2.5 | 0.60 | 1.67 |
| 3.0 | 0.67 | 1.50 |
| 3.5 | 0.71 | 1.40 |
| 4.0 | 0.75 | 1.33 |
| 4.5 | 0.78 | 1.29 |
| 5.0 | 0.80 | 1.33 |
For alternative demand elasticities, Table 3 lists the ratio of marginal revenue to price and the ratio of the consumer benefits to the monopolist's benefit. Clearly, the excess of the consumer benefit to that of the monopolist diminishes with increases in the demand elasticity, but the producer benefit is less than the consumer benefit for less than infinite elasticities.