Comprehensive Truck Size and Weight Limits Study - Modal Shift Comparative Analysis Technical Report

Appendix C: Intermodal Transportation and Inventory Cost Model

C.1 Introduction

The Intermodal Transportation and Inventory Cost (ITIC) is a computer model for performing policy analysis of issues concerning long haul freight movement, such as modal diversion or the assessment of economic benefits associated with changes in transportation policy or infrastructure. The model replicates the decision-making tradeoffs made by a logistics manager in selecting the mode and shipment size used to re-supply a company's inventory of a particular product. The implications of making alternative choices are assessed in terms of both modal choice and in dollars and cents.

C.2 About The Program

ITIC was developed to estimate the diversion potential generated by a change in the transportation levels of service or price that would likely be caused by improvements in transportation infrastructure, transportation operations, or government policy. It can also be used to calculate estimates of the economic benefits associated with such a change. The ITIC model is a disaggregate demand model. The model chooses the transportation alternative with the lowest total logistics cost. This process is repeated for a large number of disaggregate observations from a representative sample of shipper movements. The model summarizes the statistics on the analyzed sample to estimate mode share and travel demand.

The ITIC model was first developed in 1995 for the U.S. Department of Transportation's Comprehensive Truck Size and Weight Study (2000 CTSW Study). The model has undergone improvement over the years, but has remained in continuous use since its development. The ITIC model is used in the 2014 CTSW Study to estimate traffic diversion from existing truck configurations to alternative truck configurations, and to estimate the diversion of railroad traffic to the same potential vehicle configurations.

This documentation describes the ITIC model logic used for the comprehensive truck size and weight study mandated under MAP-21. The 2014 CTSW Study estimates shifts of highway freight and rail freight to trucks with alternative configurations (i.e., increased weight limits, increased cubic capacity, or increases in both weight and cubic capacity). The base-case control vehicles from which traffic shifts occur are five-axle tractor semitrailer (the control single) and five-axle twin 28-foot trailer (the control double), each with a GVW of 80,000 lbs. The alternative truck configurations and their associated gross-vehicle weight limits are five-axle tractor semitrailer at 88,000 lbs. (scenario 1); six-axle tractor semitrailer at 91,000 lbs. (scenario 2) or 97,000 lbs. (scenario 3); five-axle twin 33-ft. trailers at 80,000 lbs. (scenario 4); seven-axle triple trailers at 105,500 lbs. (scenario 5); and nine-axle triple trailers at 129,000 lbs. (scenario 6). These size and weight specification were chosen for analytical purposes only. They do not reflect weights or sizes that FHWA believes are necessarily appropriate. Other vehicle configurations could also be tested, but the user would have to supply the attributes of those configurations required by ITIC. Those attributes are described in this documentation.

The technical documentation will discuss the methodology and data utilized by the ITIC model.  The ITIC model can provide policy information assessing diversion to alternative truck configurations or rail intermodal as measured against a conventional five-axle tractor 53-foot semitrailer combination or a five-axle twin 28-foot trailer combination.

The ITIC Model Methodology

The ITIC Model uses theoretical and empirical foundations with a long history of development that has covered more than 36 years.^[11] The methodology has been used in dozens of policy studies by both government and the private sector examining changes in infrastructure, transportation operations, pricing policy, government policy, and possible advances in technology. It will be useful therefore, to describe the underlying economic theory which serves as the theoretical basis for the model, the diversion model itself, the model components and organizational structure, the databases used as input, and the processes which are used to prepare the data.

Model Overview

The model was designed as a discrete choice model for use with disaggregate freight movement databases. The approach used in the ITIC freight diversion model is based on an earlier mainframe model-the Translog Shipper Cost Model-developed by a research team at the Massachusetts Institute of Technology (MIT) Center for Transportation Studies,^[12] which has served as the conceptual design for later models. The most notable of these is the Intermodal Competition Model (ICM) employed by the Association of American Railroads for analyses of policy issues of significance to the railroad industry. While both the ITIC and ICM are discrete choice models, the ITIC and ICM differ in their approaches to the probability that a given commodity flow moves by the transport mode being analyzed. ITIC assigns all moves to the transportation alternative having the lowest total logistics cost, while the ICM is based on a continuous probability model of mode choice estimated from observed mode shares in freight markets. Where real-world transportation mode choice decisions are made primarily on differences in the logistics costs included in ITIC, ITIC would be expected to produce reliable estimates of modal shifts. This would most likely be the case for long-run truck-to-truck modal shifts after shippers and carriers have had the opportunity to adjust equipment and distribution patterns to reflect cost and other operational differences between equipment allowed under previous size and weight limits and equipment allowed under new truck size and weight limits. To the extent that factors not accounted for in the logistics costs included in ITIC influence potential shifts between rail and truck, ITIC may not be as accurate in estimating rail-to-truck mode shifts. Significant effort would be required to develop a nationwide model that reflected the influence of these other factors. This was beyond the scope of the current project.

This overview will present the theoretical basis for the model, a description of the conceptual framework within which the model system resides, and a brief review of the functions of the logistics cost module.

Theoretical Basis for the Model

Economic theory treats transportation just like any other factor used in production. The problem is that it is different, not only in terms of its nature, but also in terms of its impact on each of the other inputs. The theory of the firm is based on the assumption that each firm minimizes the costs required to produce a given quantity of output. Transportation, though only one of the factors of production, is different in that it is not consumed directly, but is a service used only in processing other inputs or outputs. If transport costs are excessive, this results in higher costs for those inputs that require transport, which in turn, results in a higher cost for the delivered product.

The neoclassical approach used by economists in modeling the behavior of shippers who face competing modes is typified by the work of Friedlaender and Spady,^[13] who begin with the observation that truck and rail transportation are only two of many inputs used by the firm in producing its basic products. In their choice of inputs they attempt to select that set which maximizes profits, using more of one input and less of another. Transportation is then, according to the neoclassical approach, just another input. The firm values each input in terms of its marginal contribution to profits.

To implement the neoclassical approach requires information not only on the transportation expenditures made by the firm, but also on all of the other inputs, including land, labor and capital. Further, this approach requires that one know all of the inputs for a particular industry and their roles in the production process. Implementing the neoclassical approach as an everyday decision analysis tool becomes unworkable without gross oversimplification. It is therefore not practical for our purposes here, though it does shed light on the manufacturing tradeoffs that are possible and the role of transportation in the process.

Other models of freight demand have been explored in the literature. In 1988, a Transportation Research Board Study of freight demand^[14] summarized the models and the freight flow data that are generally available to practitioners in this field. None of these has achieved prominence for a variety of reasons, the most important of which is that many are aggregate models. Chiang,^[15] in his doctoral dissertation, provides an explanation of the problems that are associated with most of these aggregate models:

Most of the existing freight models are correlative rather than explanatory and completely insensitive to changes in transport level-of-service measures. This is due to a number of factors; first, the data limitations. Data which can be used to undertake a careful estimation of disaggregate behavioral freight demand model are almost nonexistent. Thus, researchers in the past have been constrained to either piecing together useful aggregate data to estimate an aggregate demand model ^[16] or to using shipper surveys to estimate very limited shipper choice models. ^[17]

A second limitation comes from the fundamental difficulties which most researchers have experienced in attempting to apply economic theories of derived demand to freight demand analysis without making unattractive simplifying assumptions. One frequently used assumption is constant transport cost. That is, the freight rate is assumed not to be influenced by the quantity shipped. This makes the model policy insensitive to changes in the transportation level-of-service. In fact, in practice freight rates are a decidedly decreasing function of shipment size. There are clearly economies to the shipper to large shipment sizes.

Finally, the true cost of transport should include inventory costs as well as tariff charges which results from the logistics management process and are thus also a function of shipment size.

A second approach taken by economists and other transportation researchers is to assume that the inputs required in the production process are those already observed moving in the transport system. The traffic departments of most firms routinely record individual records concerning these shipments. As Chiang points out "It is clear that the firm is the basic decision-making unit in freight transportation." These records kept by the firm include bills of lading, carload waybills and truck freight bills. Each is an indication of the use of a product in the production process of a manufacturer, or the distribution process of a wholesale distributor, or a retail merchandiser. Different suppliers, modes, or shipment sizes are possible alternatives to the observed movement, but the use of the product as input to the firm's production process is taken as fixed. This does not seem an unreasonable assumption over the short term.

Freight demand models of this second type have been reported on by Roberts, Chiang and Ben Akiva;^[18] Winston;^[19] and others. The philosophy underlying the diversion component of these models is that the receiver is a rational economic decision maker who attempts to minimize the total cost of acquiring the inputs he needs for production; shipping them to the place he needs them in the process, storing them until their use, and protecting the company against possible shortages during the process. In short, the receiver attempts to minimize total logistics costs for the delivered product. This involves not only the selection of the mode of transport to be used, but also the selection of the supplier of the product, the choice of inventory control system, the location of warehouses and the firm's overall strategy for serving the market. The process is too complex to address in detail at this point, however, the basic theoretical foundation of the model described here is based on this concept.

Applications of This Family of Models

These findings have been incorporated into modal choice models used in a number of freight policy studies.^{[20] [21]} One such model, the Intermodal Competition Model,^[22] has been used by the Association of American Railroads to investigate the potential diversion from rail that would occur if longer combination vehicles were allowed to operate on the Nation's Interstate Highway System. In addition to the 2000 CTSW Study cited earlier, the U.S. Department of Transportation has used the ITIC model to assess rail-to-truck and truck-to-truck diversion in the Western Uniformity Scenario Analysis, a regional truck size and weight scenario requested by the Western Governors' Association^[23] and FRA's analysis of the economic benefits of positive train control.^[24]

Model Development for the MAP-21 Comprehensive Truck Size and Weight Study

Prior ITIC analyses have used Excel workbook versions of the model logic. Because Excel is limited to approximately 1 million records, which would not accommodate the disaggregated data required for the 2014 CTSW Study, statistical programing software packages were used for the analysis. Equations from existing Excel versions of ITIC, including: ITICV22 (1/25/2001 - 2000 CTSW Study); ITIC_2006 (4/7/2006 - Western Uniformity version); ITIC_5000 (3/15/2010 - developed to process smaller sample for quick turnaround analyses) were reviewed for logical consistency across the various versions. After verification of consistency with the logic appropriate for this study, the Excel workbook equations were written into World Programming System code and then translated to the free open-source R-language statistical programming language software to provide no-cost access to software capable of processing the code.

Variables Affecting Choice of Supplier, Shipment Size, and Mode

The factors influencing a shipper's choice of mode are complex and highly interdependent. They involve tradeoffs between the cost of transportation and overall transit time and delivery reliability, but there are more subtle underlying factors.^[25] Research reveals that the principal decisions in this mode selection process are those that affect the receiver of the goods rather than the shipper. Typically, the receiver is the buyer of goods, the shipper is the seller and the ownership of the goods is usually transferred legally at the time the shipment is loaded onto the conveyance. Thus, the shipper is typically the receiver's "agent" in the process and it is his wishes that are honored in the size of shipment and the choice of mode. It is therefore appropriate to view the process as involving a single decision-maker-the shipper/receiver.

The most important tradeoffs involve the annual use of a product by the receiver. High annual use of a product allows the receiver to order large replacement shipments and to take advantage of the low transport costs afforded by economies of scale in shipping associated with large shipment sizes.^[26] High value of the product imposes a penalty to ordering more than can be readily used by tying up capital in inventory. Excess inventory can be avoided by ordering product more frequently in smaller shipment sizes. Small shipment sizes carry their own penalties. Ordering is a costly process. Smaller shipment sizes typically carry high unit cost of transportation, and if the shipment size is smaller than a full vehicle load, the load must be picked up at the origin by the freight carrier and consolidated before shipment, then deconsolidated and delivered at the destination end. Most LTL, less than truckload, trucking, parcel carriers and airfreight systems perform consolidation/deconsolidation of smaller shipments into full vehicle loads. The consolidation and deconsolidation processes are also expensive, sometimes exceeding the cost of line haul transportation.

Other variables can also play an important role. The density of a product influences the choice of vehicle either by loading "heavy," in which case payload is important, or loading "light," in which case cube is more important. Shelf life influences choice of mode by placing a premium on transit time, where longer travel time leads to less time available on the grocer's shelf before the product spoils. Loss and damage may lead to a need for emergency shipments. Many variables turn out to be important to the process.

Tradeoffs Made By the Shipper/Receiver

Most of these variables affecting the choices of the receiver have been incorporated into the ITIC Model. The program develops the tradeoffs that would be made by a receiver who is attempting to minimize the total logistics costs associated with maintaining an inventory of the product for use in manufacturing or wholesale trade. The variables are used to develop each of the individual cost factors listed on the right hand side of the figure above. They include the type of receiver, variables that describe the product, information on the current mode of transport and potential new modes and the attributes of the product being carried.

These variables are used to write equations for each of the components of the receiver's total logistics costs as a function of the principal choice variables (i.e., choice of supplier, choice of mode, and choice of shipment size). Total logistics costs can be expressed in cost per unit, cost per hundredweight or annual cost. Transport charges are added to logistics costs to give the total transportation and logistics cost of the strategy. If different suppliers are considered, with different purchase costs, the total delivered cost per unit or per hundredweight is given. Most receivers will select that strategy with the minimum total delivered cost. This program can be used to examine those circumstances under which one mode will be chosen over other modes.

Truck-to-truck diversion involves decisions made by carrier management as to what equipment to use to accomplish a particular movement. By contrast, rail-to-truck, or truck-to-rail diversion involves a decision by the shipper/receiver to use another entirely different mode of transport. This "between modes" type of decision is more complex, involving the evaluation of tradeoffs in equipment availability, transit time and reliability of delivery, freight loss and damage experience and the size of the potential shipment and its suitability for movement on the mode in question. The shipper's rationale for making these decisions must be modeled if these tradeoffs are to be evaluated properly.

Cost of Movement to the Receiver

In the model, the person responsible for making the modal decision can be viewed as attempting to select that mode and shipment size which for a particular origin to destination movement will minimize the total logistics cost of the goods being shipped to the receiver. Demand for transportation service by a particular mode may grow or shrink in response to changes in service or cost, depending on its impact on the individual shippers' own business and the other alternatives available. However, the model assumes that all of the product used annually will move by one of the alternatives.

In the model these key variables may be grouped into three major groups:

1. Shipper/receiver attributes
2. Commodity attributes
3. Transport attributes

As described earlier, the most important variable appears to be one of the shipper/receiver attributes, the annual use of the product by the receiver. Clearly, rail as a mode is uniquely capable of handling larger individual shipments than truck. The typical carload can handle shipment weights up to 200,000 lbs. or more, while a maximum single unit truckload payload is around 50,000 lbs. Rail carload shipments of 100 tons are routine, and multi-car shipments of 1,200 tons or more can be handled on the same bill of lading. Unit trains moving as much as 10,000 tons (20 million lbs.) are also common. By contrast, if a shipper must take a 200,000-lb. shipment in order to use rail (instead of the 20,000-lb. shipment he would like to take), it could result in thousands of dollars of unwanted inventory cost. Shipper modal choice behavior, then, depends heavily on the amount of product used annually.

Commodity attributes are also important determinants of shipper behavior. The product being shipped determines the loading and handling requirements as well as the maximum size of shipment that can be accommodated in a given piece of equipment. These variables include:

• Density
• Value per pound
• Shelf life
• Typical packaging

The relevant product data are appended to the individual movement observation in the input data prepared by the user for input into the model. The product data represent averages developed by FHWA and FRA for use in mode choice modeling.

Variables describing the transport attributes of the modes under consideration have also proven to be important. These include:

• Transit time
• Reliability
• Loss and damage experience

These and other variables are incorporated into a "shipper's utility function" within the model. Models for estimating level of services attributes are included in the ITIC model. The obvious choice for the shipper's utility function is the "total logistics cost" associated with the ordering, transport, inventory, and use of the product being shipped. Total logistics cost is the item that the shipper is attempting to minimize when he selects one mode of transportation over another or one shipment size over another.

The components included in the shipper's total logistics cost function include:

• Ordering cost
• Capital carrying cost in transit
• Capital carrying cost in inventory
• Warehousing cost
• Loading and unloading cost
• Safety stock carrying cost
• Cost of loss and damage claims

These variables (along with a few parameters and descriptive variables) allow the total logistics costs of acquiring, shipping and storing the product to be computed by the model.

Selecting a Source of Disaggregate Data

To perform an analysis using the ITIC model, one begins by identifying potential freight movements that will be impacted by the policy change under study. If the question that is being addressed is the ability of a new intermodal service to attract existing truck moves, the disaggregate data base should be a representative sample of individual truck moves. If, on the other hand, the policy question under study is how much diversion of rail traffic is likely to occur if new, larger trucks are allowed on the roadway, the disaggregate data base should be a representative sample of rail movements. The data to be used, therefore, depends on the policy question that is being addressed. The source of potential diversions to another mode or shipment size should be used as the disaggregate sample.

Rail Carload and Intermodal Data

The Surface Transportation Board's Carload Waybill Sample (STB waybill) contains a sample of waybill shipping documents from all U.S. railroads that terminate a minimum of 4,500 revenue carloads annually. Sampling rates vary by method of reporting, manual and computerized, and the number of carloads on the shipping document. Sampling rates range from 1 percent to 20 percent for manual submissions and from 2.5 percent to 50 percent for computerized submissions. Data fields from the waybill sample provided for use in this study included:

• Record serial number
• Intermodal service code
• Rebill code
• Intermodal equipment flag
• Nominal car capacity (not used)
• AAR equipment type
• Expansion factor
• Four-digit STCC code (commodity classification and hazmat classification)
• Carloads
• Tons
• Intermodal units
• Short-line miles
• Total route distance
• Revenue
• Variable cost
• Origin county FIPS
• Destination county FIPs
• Car ownership (rail or private - not used)
• Intermodal equipment owner mark (analyzed, not used)
• Short line RR flags (originating, terminating, both, junction frequency, analyzed, not used)

Truckload Movement Data- The Freight Analysis Framework

FHWA's Office of Freight Management and Operations sponsors the Freight Analysis Framework (FAF), a derivative database of the commodity flow survey data collected by the Bureau of the Census. FAF data includes tonnage and value commodity flows between 123 geographic regions of the United States by transport mode. For this study, FAF truck flows were disaggregated to the county level to allow for detailed highway network assignment.

FAF county-to-county truck tonnage volumes were assigned to truck configuration and cargo body type using information from the 2002 VIUS. The VIUS data were analyzed by commodity, vehicle configuration, cargo body type and primary operating area (as a proxy for length of haul) to allocate FAF volumes to trucks. Table C1 shows the overall tonnage allocation by vehicle class and length of haul category.

Table C1. FAF Tonnage Allocation by Vehicle Class

Vehicle Class	< 100 Miles	100 to 200 Miles	> 200 Miles	Total
Single Unit Truck	32.6%	3.4%	1.1%	16.7%
Single Unit Truck pulling Trailer	5.6%	3.0%	1.3%	3.7%
3 & 4 Axle Tractor Semitrailer	4.3%	4.8%	0.9%	3.3%
5 Axle Tractor Semitrailer	41.5%	64.2%	89.6%	61.1%
6 Axle Tractor Semitrailer	5.9%	7.1%	1.8%	4.9%
7 and more Axle Tractor Semitrailer	1.6%	3.2%	0.0%	1.4%
5 Axle Double	4.3%	9.9%	3.8%	5.4%
6 or more Axle Double	4.3%	4.5%	1.3%	3.4%
Triple	0.0%	0.0%	0.2%	0.0%
Total	100%	100%	100%	100%

Commodity Attributes

The ITIC model uses two commodity attributes in its computations. These are the density, measured in pounds per cubic feet, and commodity value, measured in dollars per pound. In the 2000 CTSW Study, commodity density and value were read into the model from lookup tables. Density was used in the estimations of truck payload weight and storage space requirements. As described in the payload section of this documentation, density is no longer used to determine payload. And as described in the truckload movement data section, commodity value for this study was part of the FAF database used.

Annual Use of the Product

Establishing the annual level of use of a product by the receiver is one of the most problematic factors in running the ITIC model; however, we know that annual use is clearly the most important determinant of shipment size.

For truck movements or intermodal movements, the annual use is typically much smaller than for shipments by rail carload. Annual uses of less than about 250,000 lbs. per year (about five truckloads) will almost certainly go by truck, especially if the product is expensive, or the product has a short shelf life. Above 1 million lbs. per year, the low cost of transporting a 200,000-pound carload shipment by rail becomes more and more attractive. If the development of annual use rates for observed truck shipments is impossible, one could use a Monte Carlo simulation to draw representative use rates from a distribution. County Business Patterns^[27] reports by four-digit Standard Industrial Classification (SIC) code the number of firms by size that exists in each county in the United States. This can be used to help develop a typical use rate distribution for use in the process.^[28] However, implicit in the FAF, the annual use is considered to be the volume on each record.^[29]

For observed rail movements one can use the Rail Carload Waybill Sample to develop this information. By sorting the waybill data to group all of the movements of a particular commodity destined to a single point and summing the tons carried, you have a proxy for the amount of that good used by a single receiver at that point-the annual use. Obviously, the more exclusive the definition of the origin and destination (FSAC) ^[30] and the more defined the product code (seven-digit STCC), the better the result. A FSAC is the Freight Station Accounting Code used by an individual railroad. A FSAC is typically the loading or unloading point of a single receiver.

There is typically no fundamental difference between the use rates of a product traveling by trailer-on-flat-car (TOFC) rail and one moving by truckload truck. Consequently, if the policy question concerns diversion from TOFC-to-truck, or from truck-to-TOFC, the annual use rate is irrelevant because the shipment sizes that can be used by the two modes are essentially the same. The tradeoffs that matter in choosing the mode are difference in rates and service quality. At the same annual use, low value and high density would appear to favor TOFC, while high value and high cube would tend to favor truck. Container-on-flat-car (COFC) movements are typically international shipments, so these same conclusions don't necessarily hold for those movements.

Truck Payloads

The amount of product that can be carried in a truck is a consequence of the truck size and weight laws that exist at a given point in time. These laws are quite complex, involving axle loadings and their spacing as dictated by the Federal Bridge Formula.^[31] The laws are different in some of the Western States, in part because at the time the upper limit on weight was set at 80,000 lbs., these States already allowed higher weight limits. Consequently, these States were "grandfathered" at the higher weights. Travel on the Interstate Highway System beyond State borders, however, is currently limited to a total weight of 80,000 lbs. Consequently, the amount of product that can be loaded into a truck is 80,000 lbs. less the tare weight of the empty truck. For a heavy-loading commodity, like bricks for example, the payload is around 50,000 to 55,000 lbs. For a light-loading commodity like Styrofoam balls, the payload may be only 20,000 lbs. because the trailer cubes out before the weight limit is reached. It should be noted that the weigh-out vs. cube-out aspect is a function of preprocessing the data based upon the commodity weight per cubic foot and the available cubic feet for loading. The applicable truck payload weight is key to estimating the number of truck trips associated with the annual use rate.

Beginning with the analysis for the Western Uniformity Scenario, the estimation of payload has been made based on an analysis of payload weights by commodity, truck configuration, and truck body type attributes from the 2002 Vehicle Inventory and Use Survey (VIUS). While several iterations of this method did not exactly replicate the targeted weight distribution developed for study VMT control totals, it did produce a result closer to that distribution than the weigh-out cube-out payload method used in the 2000 CTSW Study.

Table C2, compares the VIUS Payload method with the Weigh-out Cube-out method in relation to the observed weight distribution from the VMT control total weight distribution. The table truncates GVW below 50,000 lbs. to eliminate empty moves from the control total distribution from the comparisons - by definition the two payload estimation method distributions include only loaded VMT. When included, control total VMT under 50,000 lbs. accounts for 40 percent of total VMT at weights between 20,000 lbs. and 50,000 lbs., some portion of which is empty movements. For the VIUS Payload Model method, 6 percent of total loaded VMT is at weights between 30,000 lbs. and 50,000 lbs. The control total VMT includes 10 percent of loaded VMT above 80,000 lbs. and the VIUS payload method yields 13 percent of loaded VMT above 80,000 lbs. The ITIC Weigh-out Cube-out Method yields no loaded VMT below 60,000 lbs. or above 80,000 lbs.

Table C2. VMT, Payload, and Weight Distributions

Weight Group Upper Bound	Control Total CS5 VMT (millions)			VIUS Payload Weight Distributions CS5 VMT (millions)			Weigh-out Cube-out Weight Distributions CS5 VMT (millions)
	VMT	Percent	Cumulative Percent	VMT	Percent	Cumulative Percent	VMT	Percent	Cumulative Percent
50,000	19,990	20	20	4,841	5	5%	0	0	0
60,000	18,237	19	39	10,254	11	16%	105	0	0
70,000	21,158	22	61	21,162	23	39%	9,952	12	12
78,000	23,537	24	85	35,134	38	77%	13,957	17	30
80,000	4,817	5	90	9,466	10	87%	56,639	70	100
over 80,000	10,276	10	100	12,010	13	100%	0	0	100
Total VMT	98,016			92,866			80,653

The results of this comparison indicate that the amount of actual Combination-Tractor-Single Trailer, 5-axle configuration (CS5) travel of loaded VMT with GVW of between 78,000 lbs. and 80,000 lbs., as captured by weigh-in-motion data, is on the order of 5 percent, while the weigh-out cube-out method produces a share of about 70 percent. Since the VIUS Payload method for estimating payloads and distributing operating weights comes closer to the observed weight distribution of CS5 vehicles, that method was used in this study rather than the weigh-out cube-out method used in the 2000 CTSW Study.

Truckload Trucking Rates

Truckload rates for dry van movements are extremely competitive throughout North America. Although there is a great deal of spread in observed rates, even on the same traffic lane, overall rates appear to reflect the repositioning costs needed to correct equipment imbalances. In the real world, competition drives the rates to adjust for these load imbalances. The rates observed for truckload movement in each city-pair market tend to reflect this phenomenon. This occurs because the number of loaded trucks moving into some regions is larger than the number of loads desiring to move out. Trucks carrying goods out of an equipment surplus region typically charge a lower rate because they know they will have a difficult time securing outbound loads and must either lower their outbound prices or wait longer to get a load. When more loads move out of a region than move in, there is typically a shortage of equipment. Shippers are willing to pay more to attract a carrier. Consequently, outbound rates from an equipment deficit region are typically higher.

FHWA purchased a truckload rate database from Class 8 Solutions. The data captured dry van truckload rates between locations in the United States that were divided into 120 markets, which were used in the Western Uniformity and subsequent studies. Although these data were proprietary, FHWA obtained an agreement from the successor to Class 8 Solutions' licensing rights, Trans-Research International, to include rates averaged over state-to-state origin-destination pairs in the ITIC-ST version of the ITIC model that was made available to the public. 

The truckload rate database consisted of CS-5 dry-van truckload rates for 2005 between the 120 markets contained in the database. Individual counties were assigned to the appropriate database market by matching the three-digit prefix zip code for the county seat to the three-digit zip code market assignment provided by the vendor. For initial use in the Western Uniformity Scenario, rate differentials for different body types - Flatbed, Refrigerated and Bulk - were developed from differences in operating characteristics, such as empty/loaded mileage ratios, and equipment costs. Similarly, rate differentials for different configurations were developed from equipment cost data. For the 2014 CTSW Study, those rates used in the Western Uniformity Scenario were inflated from 2005 to 2011 by 17 percent, the change in the Bureau of Labor Statistics Producer Price Index for General Freight Trucking between 2005 and 2011. The resulting county-to-county rates were then aggregated by origin-destination state and grouped into mileage blocks of 25 miles. A tonnage volume weighted average rate was then calculated for state-to-state flows within each mileage block. In this manner, moves of similar distance between states; for example Guilford County, NC (Greensboro) and Davidson County, TN (Nashville) and Buncombe County, NC (Asheville) and Shelby County, TN (Memphis) would have the same state-based rate but would not reveal the more detailed rate information between the 120 market divisions in the database.

Figure C1 below shows the Study's average 2011 rates for dry-van, flat-bed and refrigerated service as compared to publically available monthly data during the same time frame. As the graph shows, the rates used for the study fall within the range of rates observed over the course of the year.

Figure C1. 2011 Rates

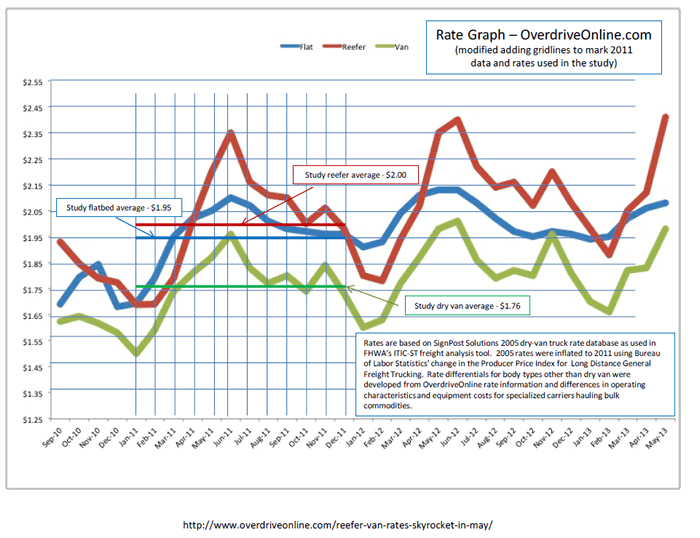
Rail Carload Rates

The Surface Transportation Board's Carload Waybill Sample (STB waybill) contains a sample of waybill shipping documents from all United States railroads that terminate a minimum of 4,500 revenue carloads annually. Sampling rates vary by method of reporting (i.e., manual and computerized) and the number of carloads on the shipping document. Sampling rates range from 1 percent to 20 percent for manual submissions and from 2.5 percent to 50 percent for computerized submissions.

Revenues on individual records of the waybill sample may misrepresent rate adjustments as annual volume thresholds are met or other factors that are not transparent to the user of waybill data. For example, Wolfe and Linde cite 56 waybill records on the 1988 Public Use sample of unit train moves of wheat from Oklahoma City BEA to Houston BEA with revenue per car mile ranging from $3.41 per mile to less than $0.03 per mile.^[32] For this study, the revenues and variable costs of all records of the same four-digit STCC commodity, moving the same distance between the same origin and destination in the same rail car type are combined and divided by the car-miles generated by those moves to calculate consistent revenue and variable costs per car-mile for the analysis. This treatment provides a transportation cost that is consistent with the single truck rate applied to all moves in the same equipment type between the same origin and destination.

Rail Intermodal Rates

Similar to carload records, waybill revenues for intermodal records moving between the same origin and destination in the same car type service show significant variance that may mask information regard volume discounts or other factors. Confounding the issue of revenues on intermodal records is the service provide by the carrier, as indicated on the Service Plan Code. Railroads provide service that ranges from ramp-to-ramp service, where the dray at neither end is included in the service provided, to door-to-door service, where the dray at both ends is included in the service. For purposes of this study, intermodal rates were developed from waybill records with ramp-to-ramp service. A drayage fee of $225 at both origin and destination was added to the rail transportation cost to arrive at the door-to-door transportation cost of intermodal. This amount corresponds to the minimum charge truck-load rate and isn't inconsistent with an on-line drayage rate calculator for a dray distance between 20 and 40 miles.

Rail Variable Cost

Rail variable costs play a role in deciding what traffic to accept and what to reject. When intermodal rates calculated by the model from the procedure described above fall below 110 percent of rail variable costs, plus drayage costs for the move, the load is refused by rail and allowed to select truck at its original truck rate. Variable cost is increased to assure a minimum contribution to the railroad's overhead. These figures are used to limit possible diversion to the rail mode. Clearly, rail management does not want to compete aggressively to attract (or to hold on to) traffic where the revenues are below short-term variable costs. Also, including drayage costs in the acceptance threshold assures that inordinately distant, and consequently costly, shipment origins/destinations from intermodal terminals will be rejected. The rail variable costs included in the ITIC database were estimated using cost data from Reebie Associates (currently Global Insight) and then modified to include box costs. The rail variable cost range from 80 cents per mile in the under 500 mile segment to 47 cents per mile for 1500 miles and up. These costs vary by the traffic density (annual rail shipments) and distance between selected rail corridors.

Data that is not included

In a true disaggregate methodology, the "proof" that a shipment of a given size went by a certain mode is typically documented by either paper or electronic record of the movement. A waybill, or freight bill, shows the date of the shipment, the name of the shipper, the name of the receiver, the origin and destination, the size of shipment, the mode, the freight changes, and any special handling requirements. What is not typically available is the level of service variables that prevailed on the observed mode at the time of the shipment. The ITIC allows a user to easily change these factors to test alternative service variables. These must be inferred from the mileage, the conditions of transit, any terminal operations that were known to occur, etc. Also missing on the freight bills are the total tons of the product used annually by this receiver. The disaggregate input data file must contain all of this data with estimates of those data elements that are missing from the paper record.

Benefits Analysis

The direct economic benefits of a policy change that impacts the logistics cost of shippers can be developed directly from the model output. This is possible because the model measures the change in the shipper/receiver utility function in dollar terms caused by shifting from using one alternative to using another. The logistics cost savings is the direct dollar saving to the shipper of making the shift.^[33] When aggregated over all shippers it is the first round economic impact of the policy change. If, for example, a new TOFC service is able to attract users away from their existing mode of transportation, the change in the total logistics cost of shifting to the new, lower cost mode is fully reflected in the shipper's reduced total logistics costs. By aggregating this savings over all shippers, the entire initial dollar saving of the shipping community is developed. This saving will be reflected in the company's profitability and can be saved as retained earnings, kept by the owners, passed on to customers in the form of lower prices, or used to hire new staff and expanding the productive capacity of the firm.

It should be noted that the first round economic impact is just that-a first round. Once the savings has been distributed, it could result in further growth in the economy of the trading regions. The best way to measure these secondary and tertiary economic impacts is to employ one of the macroeconomic models that can use the logistics savings outputs of the ITIC model as an input to the macroeconomic model and trace the flow of economic impacts that emanate from this first set of economic savings.

Further Research and Data Needs

A key component of allocating FAF commodity volumes to individual truck trips is shipment size. As discussed previously, determining shipment size using a weigh-out cube-out logic results in GVWs that are skewed to the 80,000-lb. maximum weight limit, contrary to the weight distribution derived from observed WIM data. Although the commodity flow survey instrument includes shipment weight, this information has not been published by commodity since the 1997 survey, and even then in weight ranges too broad to be useful in determining payload weights. Including cargo body type on the survey and publishing shipment weights at a greater level of detail than in the past would provide much needed information in allocating the aggregate commodity flows to individual truck trips.

Development of a continuous probability model could improve the predictive capability of the model, particularly for estimates of modal shifts between rail and truck.

previous | next