Table of Contents

Empirical Studies on Traffic Flow in Inclement Weather

Appendix B: Model Formulation

The functional form that is utilized in this study is the Van Aerde nonlinear functional form that was proposed by Van Aerde (Van Aerde 1995) and Van Aerde and Rakha (Van Aerde and Rakha 1995), which is formulated as:

h subscript n equals the sum of c subscript 1 plus the product of c subscript 3 times u subscript n plus the quotient of c subscript 2 divided by the difference of u subscript f minus u subscript n.. [7]

As was demonstrated by Rakha and Crowther (2002) this functional form amalgamates the Greenshields and Pipes car-following models where hn is the spacing or distance headway (km) between vehicle n and vehicle n-1 in the same lane, un is the speed of vehicle n (km/h), uf is the facility free-flow speed (km/h), c1 is a fixed distance headway constant (km), c2 is a variable headway constant (km2/h), and c3 is a variable distance headway constant (h-1). This combination provides a linear increase in vehicle speed as the distance headway increases with a smooth transition from the congested to the uncongested regime. This combination provides a functional form with four degrees of freedom by allowing the speed-at-capacity (uc) to differ from the free-flow speed (uf), which is a common assumption in a number of models, including the Pipes and Gipps model, or half the free-flow speed, as is the case with Greenshields model. Specifically, the first two parameters of Equation [7] provide the linear increase in the vehicle speed as a function of the distance headway, while the third parameter introduces curvature to the model and imposes a constraint on the vehicle’s speed to ensure that it does not exceed the facility free-flow speed through the use of a continuous function. Demarchi (2002) demonstrates that by considering three boundary conditions the model constants can be computed as:

c subscript 1 equals the product of the quotient of u subscript f divided by the product of k subscript j times the square of u subscript c, times the difference of the product of 2 times u subscript c minus u subscript f. c subscript 2 equals the product of the quotient of u subscript f divided by the product of k subscript j times the square of u subscript c, times the square of the difference of u subscript f minus u subscript c. c subscript 3 equals the difference of the quotient of 1 divided by q subscript c minus the quotient of u subscript f divided by the product of k subscript j times the square of u subscript c.. [8]

Ignoring differences in vehicle speeds and headways within a traffic stream and considering the relationship between traffic stream density and traffic spacing, the speed-density relationship can be derived as:

k equals the quotient of 1 divided by the sum of c subscript 1 plus the quotient of c subscript 2 divided by the difference of u subscript f minus u, plus the product of c subscript 3 times u., [9]

where k is the traffic stream density (veh/km) and u is the traffic stream space-mean speed (km/h) assuming that all vehicles are traveling at the same average speed (by definition given that the traffic stream is in steady-state). A more detailed description of the mathematical properties of this functional form can be found in the literature (Rakha and Crowther 2002; Van Aerde and Rakha 1995), as can a discussion of the rationale for its structure.

Of interest is the fact that Equation [9] reverts to Greenshields’ linear model, when the speed-at-capacity and density-at-capacity are both set equal to half the free-speed and jam density, respectively (i.e., uc=uf/2 and kc=kj/2). Alternatively, setting the speed-at-capacity to the free-speed (uc=uf) results in the linear Pipes model given that

c subscript 1 equals the quotient of 1 divided by k subscript j, which equals h subscript j. c subscript 2 equals zero. c subscript 3 equals the difference of the quotient of 1 divided by q subscript c minus the quotient of 1 divided by the product of k subscript j times u subscript f..

The wave speed at jam density (denoted as wj) can be computed by differentiating the speed-density relationship with respect to density at jam density, to be

w subscript j equals k subscript j times the derivative of u with respect to k evaluated at k subscript j, which equals negative h subscript j times the derivative of u with respect to h evaluated at h subscript j. .[10]

By applying Equation [10] to [9] we derive

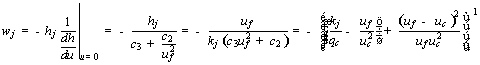w subscript j equals negative h subscript j times 1 over the derivative of h with respect to u evaluated at u equals 0, which equals the negative quotient of h subscript j divided by the sum of c subscript 3 plus the quotient of c subscript 2 divided by the square of u subscript f, which equals the negative quotient of u subscript f divided by the product of k subscript j times the sum of the product of c subscript 3 times the square of u subscript f plus c subscript 2, which equals the negative reciprocal of the following expression: the sum of the difference of the quotient of k subscript j divided by q subscript c minus the quotient of u subscript f divided by the square of u subscript c, plus the quotient of the square of the difference of u subscript f minus u subscript c divided by the product of u subscript f times the square of u subscript c.. [11]

Considering, a typical lane capacity of 2,400 veh/h, a free-flow speed of 110 km/h (which is typical of U.S. highways), and a jam density of 140 veh/km/lane, the wave velocity at jam density ranges between approximately -11.5 to -20.3 km/h, when the speed-at-capacity is varied from 80 to 100 percent the free-flow speed (which is typical on North American freeways).

As was demonstrated earlier, the Van Aerde model reverts to the Pipes linear model when the speed-at-capacity is set equal to the free-flow speed. Consequently, it can be demonstrated that under this condition the wave speed of reverts to

w equals the negative quotient of the product of q subscript c times u subscript f divided by the difference of the product of k subscript j times u subscript f minus q subscript c. , [12]

which is the speed of the linear model. Furthermore, when uc=uf/2 and kc=kj/2 the wave speed at jam density is consistent with the Greenshields model estimates and is computed as

w subscript j equals negative u subscript f.. [13]

If we consider the Van Aerde functional form the optimization model can be formulated as

Minimize E equals the summation over i of the sum of the square of the quotient of the difference of u subscript i minus u overcaret subscript i divided by u overtilda, plus the square of the quotient of the difference of q subscript i minus q overcaret subscript i divided by q overtilda, plus the square of the quotient of the difference of k subscript I minus k overcaret subscript I divided by k overtilda such that k overcaret subscript i equals the quotient of 1 divided by the sum of c subscript 1 plus the quotient of c subscript 2 divided by the difference of u subscript f minus u overcaret subscript i, plus the product of c subscript 3 times u overcaret subscript i for all i. q overcaret subscript i equals the cross-product of k overcaret subscript i and u overcaret subscript i for all i. q overcaret subscript i, k overcaret subscript i, and u overcaret subscript i are greater than or equal to 0, for all i. u overcaret subscript i is less than u subscript f for all i.. [14]

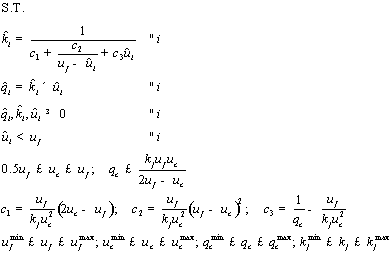Half of u subscript f is less than or equal to u subscript c, which is less than u subscript f. q subscript c is less than or equal to the quotient of the product of k subscript j times u subscript f times u subscript c divided by the difference of the product of 2 times u subscript f minus u subscript c. c subscript 1 equals the product of the quotient of u subscript f divided by the product of k subscript j times the square of u subscript c, times the difference of the product of 2 times u subscript c minus u subscript f. c subscript 2 equals the product of the quotient of u subscript f divided by the product of k subscript j times the square of u subscript c, times the square of the difference of u subscript f minus u subscript c. c subscript 3 equals the difference of the quotient of 1 divided by q subscript c minus the quotient of u subscript f divided by the product of k subscript j times the square of u subscript c. u subscript f superscript min is less than or equal to u subscript f, which is less than or equal to u subscript f superscript max. u subscript c superscript min is less than or equal to u subscript c, which is less than or equal to u subscript c superscript max. q subscript c superscript min is less than or equal to q subscript c, which is less than or equal to q subscript c superscript max. k subscript j superscript min is less than or equal to k subscript j, which is less than or equal to k subscript j superscript max. [15]

Where ui, ki, and qi are the field observed space-mean speed, density, and flow measurements, respectively. The speed, density, and flow variables with hats (^) are estimated speeds, densities, and flows while the tilde variables (~) are the maximum field observed speed, density, and flow measurements. All other variables are defined as was done earlier in describing the Van Aerde functional form.

The objective function ensures that the formulation minimizes the orthogonal error between the field observations and the functional relationship – in this case the Van Aerde functional form. The distances are normalized in order to ensure that the objective function is unitless in order to minimize an objective function over different domains. The initial set of constraints, which is nonlinear, ensures that the Van Aerde functional form is maintained, while the second set of constraints is added to constrain the third dimension, namely the flow rate. The third and forth set of constraints guarantees that the results of the minimization formulation are feasible. The fifth set of constraints, ensures that the four parameters that are selected do not result in any inflection points in the speed-density relationship (i.e., it ensures that the density at any point is less than or equal to the jam density). A detailed derivation of the final constraint is provided elsewhere (Rakha 2006). The sixth set of equations provides estimates for the three model constants based on the roadway’s mean free-flow speed (uf), speed-at-capacity (uc), capacity (qc), and jam density (kj). The final set of constraints provides a valid search range for the four traffic stream parameters that are being optimized (uf, uc, qc, and kj).

A heuristic tool was developed (SPD_CAL) and described elsewhere to calibrate traffic stream models. The procedure can be summarized briefly as follows:

  1. Aggregate the raw data based on traffic stream density bins in order to reduce the computational space.
  2. Initialize the four traffic stream parameters uf, uc, qc, and kj, and call them uf0, uc0, qc0, and kj0.
  3. Construct the model functional form and move along the functional form at increments of Δk to compute the objective function. The accuracy of the objective function computation and the computational speed will depend on the size of the Δk variable.
  4. Vary the four parameters ufi, uci, qci, and kji at iteration i from ufmin, ucmin, qcmin, and kjmin to ufmax, ucmax, qcmax, and kjmax at increments of ufinc, ucinc, qcinc, and kjinc.
  5. Construct the model functional form for each parameter combination and move along the function form at increments of Δk/i to compute the objective function. Note that the computational accuracy increases as the iteration number increases.
  6. Compute the set of parameters ufi, uci, qci, and kji that minimize the objective function.
  7. Reduce the search window by a factor of 1/i and compute ufmin, ucmin, qcmin, and kjmin to ufmax, ucmax, qcmax, and kjmax at increments of ufinc, ucinc, qcinc, and kjinc.
  8. Go to step 3 and continue until either the number of iterations is satisfied or the minimum change in objective function is satisfied.

Figure B.1 Van Aerde Model Fit to Freeway Data (Twin Cities, USA)

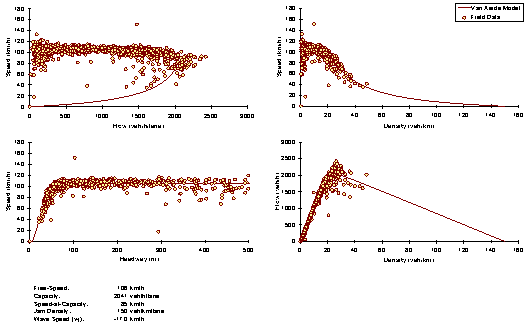
This figure presents four plots of field data and the Van Aerde model on the following axes: speed-flow, speed-density, speed-headway, and flow-density. The figure also lists values for the following parameters: free-speed is 106 kilometers per hour, capacity is 2041 vehicles per hour per lane, speed-at-capacity is 85 kilometers per hour, jam density is 150 vehicles per kilometer per lane, wave speed is -17 kilometers per hour.

The fit to five-minute data from the Twin Cities, Minnesota, demonstrates that the calibration tool is able to capture the functional form of the data. The figure clearly demonstrates the effectiveness of the proposed calibration tool together with the Van Aerde functional form to reflect steady-state traffic stream behavior on this facility over multiple regimes.

Office of Operations